An Introduction to the RSTr Package • RSTr

Overview

The RSTr package is a tool that provides a host of Bayesian spatiotemporal models in conjunction with C++ to quickly and easily generate spatially-smoothed age-standardized estimates for your spatial data. This vignette introduces you to the basics of the RSTr package and shows you how to apply the basic functions to the included example data to get small area estimates.

Models

The models provided in the RSTr package are based on the Besag, York, and Mollié (1991) Conditional Autoregressive (CAR) model, which spatially smooths data by incorporating information such as event and population counts from neighboring geographic units (counties, census tracts, etc.). The degree of spatial smoothing is determined by a spatial region’s respective population size. The CAR model can be extended to several levels of complexity, depending on the input data:

BYM CAR (CAR): Spatially smooths across geographies;
Restricted CAR (RCAR): Spatially smooths across geographies and prevents over-smoothing;
Multivariate CAR (MCAR): Spatially smooths across geographies and sociodemographic groups; and
Multivariate Spatiotemporal CAR (MSTCAR): Spatially smooths across geographies, sociodemographic groups, and time periods.

For this vignette, we will demonstrate RSTr’s functionality with an MSTCAR model.

Restricted models to prevent over-smoothing

A problem with CAR models pointed out by Quick, et al. (2021) is that of over-smoothing due to the informativeness of the BYM model. The RSTr package provides enhancements to the CAR models for both Poisson- and binomial-distributed data that prevent over-smoothing by restricting model informativeness through the rcar() function. Enhancements for the MCAR and MSTCAR models are under progress, and will be incorporated into the RSTr package as they are developed.

Datasets

RSTr comes with three main datasets: miheart, miadj, and mishp. miheart and miadj are related to the necessary components of our models, and mishp is a shapefile that helps map your results. To run an MSTCAR model, two components are necessary:

Event counts for a parameter of interest, stratified by region, group, and time period, and its corresponding population counts. These data may be binomial- or Poisson-distributed. The example dataset is binomial-distributed myocardial infarction deaths in six age groups from 1979-1988 in Michigan. Reference miheart to see how this data looks or ?miheart for more information on the dataset. For more information on preparing your event data, read vignette("RSTr-event").
An adjacency structure for your data. This is a list that tells RSTr which regions are neighbors of one other based on their region index (i.e., the order they appear in the dataset). Reference miadj for an example adjacency structure list. For more information on preparing your adjacency data, read vignette("RSTr-adjacency").

Some quick notes about data setup:

Event/population data must be organized in a very specific manner. RSTr’s models can accept up to three-dimensional arrays: in the MSTCAR model, for example, spatial regions must be on the rows, socio/demographic groups must be on the columns, and time periods must be on the matrix slices. Additionally, your event data’s regions should be listed in the same order in your adjacency structure data.
Every region must have at least one neighbor. The adjacency structures must be listed in the same order as your count data.

Functions

RSTr comes with a set of functions to generate small area estimates from your dataset. Here is a brief overview of the basic functions and their purpose:

*car(): Inputs data and model specifics and creates a local folder with all associated files to prepare for sample generation;
age_standardize(): Generates age-standardized estimates based on user-specified age groups;
suppress_estimates(): Suppresses estimates based on reliability criteria; and
get_estimates(): Creates a long table containing information on each region/group/time in the model.

Example Model

`mstcar()`

With an understanding of the example datasets and the functions, we can start running our first model. The example datasets are set up to run out-of-the-box:

mod_mst <- mstcar(
  name = "my_test_model",
  data = miheart,
  adjacency = miadj,
  dir = tempdir(),
  seed = 1234
)
#> Starting sampler on Batch 1 at Fri Dec 19 00:10:44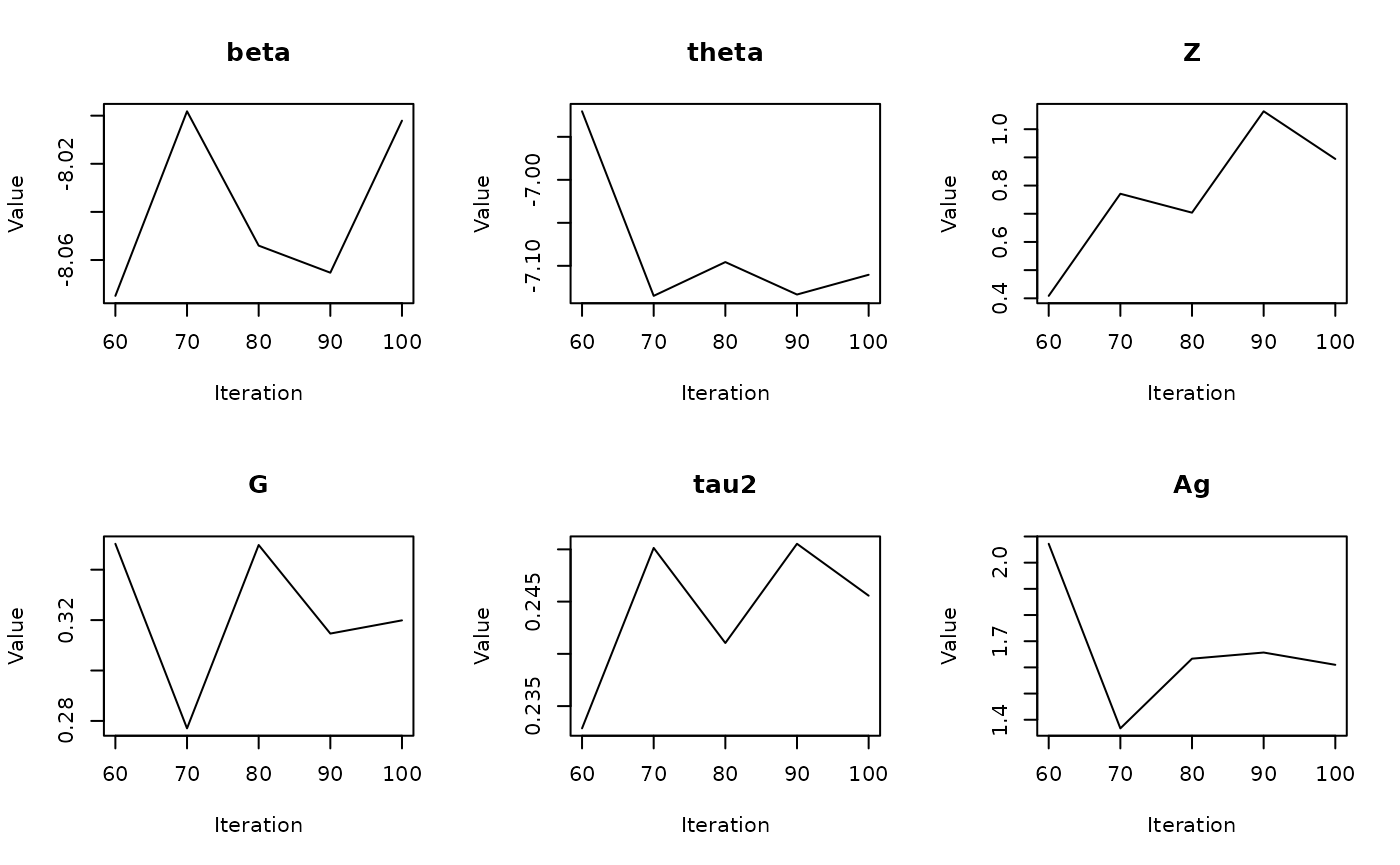

#> Generating estimates...
#> Model finished at Fri Dec 19 00:11:10

Here, we use the mstcar() function to specify our model. mstcar() accepts a few different arguments in this case:

The name argument specifies the folder where the model data lives;
The data argument specifies event/population data;
The adjacency argument specifies our adjacency structure;
The dir argument specifies the directory where to save the folder; and
The seed argument specifies a random seed for replicability purposes.

mstcar() creates a folder named my_test_model in R’s temporary directory containing folders that will hold batches of outputs for each parameter update. Additionally, an RSTr object which holds all information associated with the model (aside from samples) is created in the R environment and in the temporary directory. No samples are saved in the R environment because, given a sufficiently large dataset, MSTCAR models can become so large that it’s impossible to hold all the model samples in RAM. Therefore, all of the samples are saved locally. Should you want to save your model somewhere besides the temporary directory for future use, you can specify a folder with the dir argument.

Note that mstcar() accepts more arguments than are used here, but these are the only ones needed to get started. Priors and initial values, for example, can be specified manually, but this is outside the scope of this vignette. There will also be checks performed on the input data: if something is wrong, warnings and error messages will tell you what is wrong and how to fix it. For a list of diagnostic errors and what they mean, read vignette("RSTr-troubleshooting").

The RSTr package works by generating samples in batches and saving them locally inside of the model directory to be retrieved once the model is finished running. Generating samples in batches helps facilitate the tuning of the underlying MCMC algorithm and helps avoid computational burden by only holding a fraction of the total samples in memory at any given time. RSTr runs 6,000 iterations split into 60 batches of size 100 each. All batches are thinned for every 10 iterations by default, as the lambdas (a.k.a., the rate estimates) tend to exhibit autocorrelation. Moreover, thinning saves space when writing samples to the hard drive, as batches from larger models can balloon to gigabytes of size before thinning.

Console outputs will show the current batch number, the progress within that batch, and the elapsed time. The model Rds file will be updated as the sampler progresses in case you need to reload your model at a later date. If the model crashes for any reason or R closes while the model is being run, the model Rds file will keep track of the current batch and pick back up where it left off when re-run. While mstcar() is running, the R plot window will show traceplots from a selection of estimates to check stability and diagnose any potential issues.

If you want to learn more about mstcar() and the other model functions, read vignette("RSTr-car").

`get_estimates()`

mstcar() takes care of the vast majority of model preparation: within the function, the model is set up, samples are generated, and our medians are estimated. Once the function finishes, we can get an overview of our model:

mod_mst
#> RSTr object:
#> 
#> Model name: my_test_model 
#> Model type: MSTCAR 
#> Data likelihood: binomial 
#> Estimate Credible Interval: 95% 
#> Number of geographic units: 83 
#> Number of samples: 6000 
#> Estimates age-standardized: No 
#> Estimates suppressed: No

Here, we get a birds-eye-view of the model, including the model we used (MSTCAR), the data likelihood type, the number of geographic units, and whether our estimates have been age-standardized or suppressed along reliability criteria. With the get_estimates() function, we can get a more detailed look at our estimates. For this type of mortality data, it is common to observe the rates per 100,000 population, so we set the rates_per argument in get_estimates() to 1e5:

mst_estimates <- get_estimates(mod_mst, rates_per = 1e5)
head(mst_estimates)
#>   county group year  medians ci_lower  ci_upper  rel_prec events population
#> 1  26001 35-44 1979 41.98634 29.79605  56.17417 1.5917110      1        964
#> 2  26003 35-44 1979 51.00178 37.86450 119.49006 0.6248260      1       1011
#> 3  26005 35-44 1979 23.76272 16.29719  33.58478 1.3745537      0       9110
#> 4  26007 35-44 1979 33.61042 24.15788  45.44376 1.5790005      0       3650
#> 5  26009 35-44 1979 29.70584 22.96456  39.27994 1.8207267      0       1763
#> 6  26011 35-44 1979 38.17390 24.89862  65.99126 0.9289717      0       1470

The mst_estimates object contains in-depth information about our model estimates, including the medians, the credible intervals, the relative precisions, and the event/population counts; region, group, and time period columns are also provided.

`age_standardize()`

One of the most important features of the RSTr package is the ability to easily generate age-standardized estimates. Let’s say we want to get age-standardized estimates for the 35-64 age group; for our model, we use the age_standardize() function, then specify the groups of interest, their associated standard populations, and the name we want to give them. Since we are using data from 1979-1988, we can use 1980 standard populations from NIH to generate a std_pop standard population vector:

std_pop <- c(68775, 34116, 9888)
mod_mst <- age_standardize(mod_mst, std_pop, new_name = "35-64", groups = c("35-44", "45-54", "55-64"))
mod_mst
#> RSTr object:
#> 
#> Model name: my_test_model 
#> Model type: MSTCAR 
#> Data likelihood: binomial 
#> Estimate Credible Interval: 95% 
#> Number of geographic units: 83 
#> Number of samples: 6000 
#> Estimates age-standardized: Yes 
#> Age-standardized groups: 35-64 
#> Estimates suppressed: No

Notice now that the mod_mst object indicates we have age-standardized our estimates and the names of our age-standardized groups.

mst_estimates_as <- get_estimates(mod_mst)
head(mst_estimates_as)
#>   county group year   medians  ci_lower  ci_upper rel_prec events population
#> 1  26001 35-64 1979 107.15247  87.92325 127.88946 2.681076      7       3353
#> 2  26003 35-64 1979 146.65258 119.93045 195.45817 1.941706     12       3105
#> 3  26005 35-64 1979  71.08941  57.78063  81.64427 2.978984     27      23926
#> 4  26007 35-64 1979  87.54041  73.16101 109.51904 2.407732     15      10000
#> 5  26009 35-64 1979  88.98631  74.88835 107.03585 2.768063     11       5152
#> 6  26011 35-64 1979 112.27379  92.11683 145.85171 2.089402      8       4517

Now, get_estimates(mod_mst) shows the age-standardized estimates. Should you want to see those instead, you can set the argument standardized = FALSE.

`suppress_estimates()`

While the main benefit of RSTr is generating reliable estimates from small-population areas, we cannot guarantee that all estimates generated by mstcar() will be reliable. Therefore, it is prudent to suppress estimates that are deemed unreliable. For MSTCAR models, we can use two criteria to test for reliability: relative precision (i.e., the ratio of the median estimate to the width of its credible interval) and population count. For relative precisions, we aim for a value of at least 1 (i.e., the median is larger than the width of its credible interval), and for myocardial infarction death rates, we typically aim for a population threshold of at least 1,000. Using the suppress_estimates() function, we can generate suppressed estimates for our age-standardized rates:

mod_mst <- suppress_estimates(mod_mst, threshold = 1e3)
mod_mst
#> RSTr object:
#> 
#> Model name: my_test_model 
#> Model type: MSTCAR 
#> Data likelihood: binomial 
#> Estimate Credible Interval: 95% 
#> Number of geographic units: 83 
#> Number of samples: 6000 
#> Estimates age-standardized: Yes 
#> Age-standardized groups: 35-64 
#> Estimates suppressed: Yes 
#> Number of reliable age-standardized rates: 819 / 830 (98.7%)
mst_estimates_as <- get_estimates(mod_mst)
head(mst_estimates_as)
#>   county group year   medians medians_suppressed  ci_lower  ci_upper rel_prec
#> 1  26001 35-64 1979 107.15247          107.15247  87.92325 127.88946 2.681076
#> 2  26003 35-64 1979 146.65258          146.65258 119.93045 195.45817 1.941706
#> 3  26005 35-64 1979  71.08941           71.08941  57.78063  81.64427 2.978984
#> 4  26007 35-64 1979  87.54041           87.54041  73.16101 109.51904 2.407732
#> 5  26009 35-64 1979  88.98631           88.98631  74.88835 107.03585 2.768063
#> 6  26011 35-64 1979 112.27379          112.27379  92.11683 145.85171 2.089402
#>   events population
#> 1      7       3353
#> 2     12       3105
#> 3     27      23926
#> 4     15      10000
#> 5     11       5152
#> 6      8       4517

mod_mst now shows us that our estimates are suppressed and indicates the number of reliable rates.

If you want to learn more about get_estimates(), age_standardize(), and suppress_estimates(), read vignette("RSTr-estimates").

Illustrative Example: Mapping Estimates

We can get a better picture of the geographic patterns in our data with a map. Using ggplot (or your favorite mapping package), Let’s see how the (non-age-standardized) estimates were smoothed:

library(ggplot2)
# Original Myocardial Infarction Death Rates in MI, Ages 35-64, 1988
estimates_88 <- mst_estimates_as[mst_estimates_as$year == "1988", ]
estimates_3564 <- estimates_88[estimates_88$group == "35-64", ]
raw_3564 <- (estimates_3564$events / estimates_3564$population * 1e5)
ggplot(mishp) +
  geom_sf(aes(fill = raw_3564)) +
  labs(
    title = "Raw Myocardial Infarction Death Rates in MI, Ages 65 and up, 1988",
    fill = "Deaths per 100,000"
  ) +
  scale_fill_viridis_c() +
  theme_void()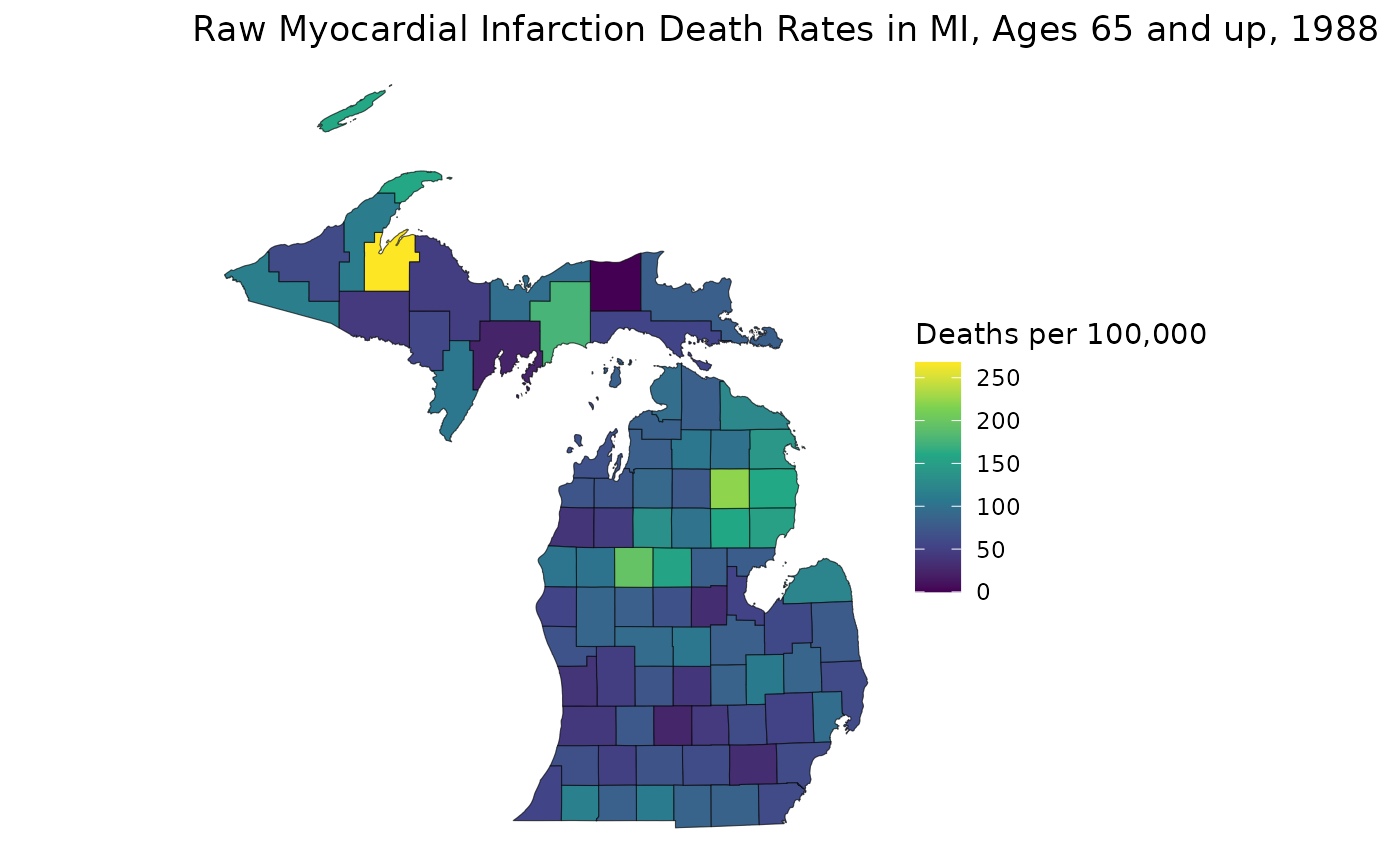

# Spatially Smoothed MI Death Rates in MI
est_3564 <- estimates_3564$medians
ggplot(mishp) +
  geom_sf(aes(fill = est_3564)) +
  labs(
    title = "Smoothed Myocardial Infarction Death Rates in MI, Ages 35-64, 1988",
    fill = "Deaths per 100,000"
  ) +
  scale_fill_viridis_c() +
  theme_void()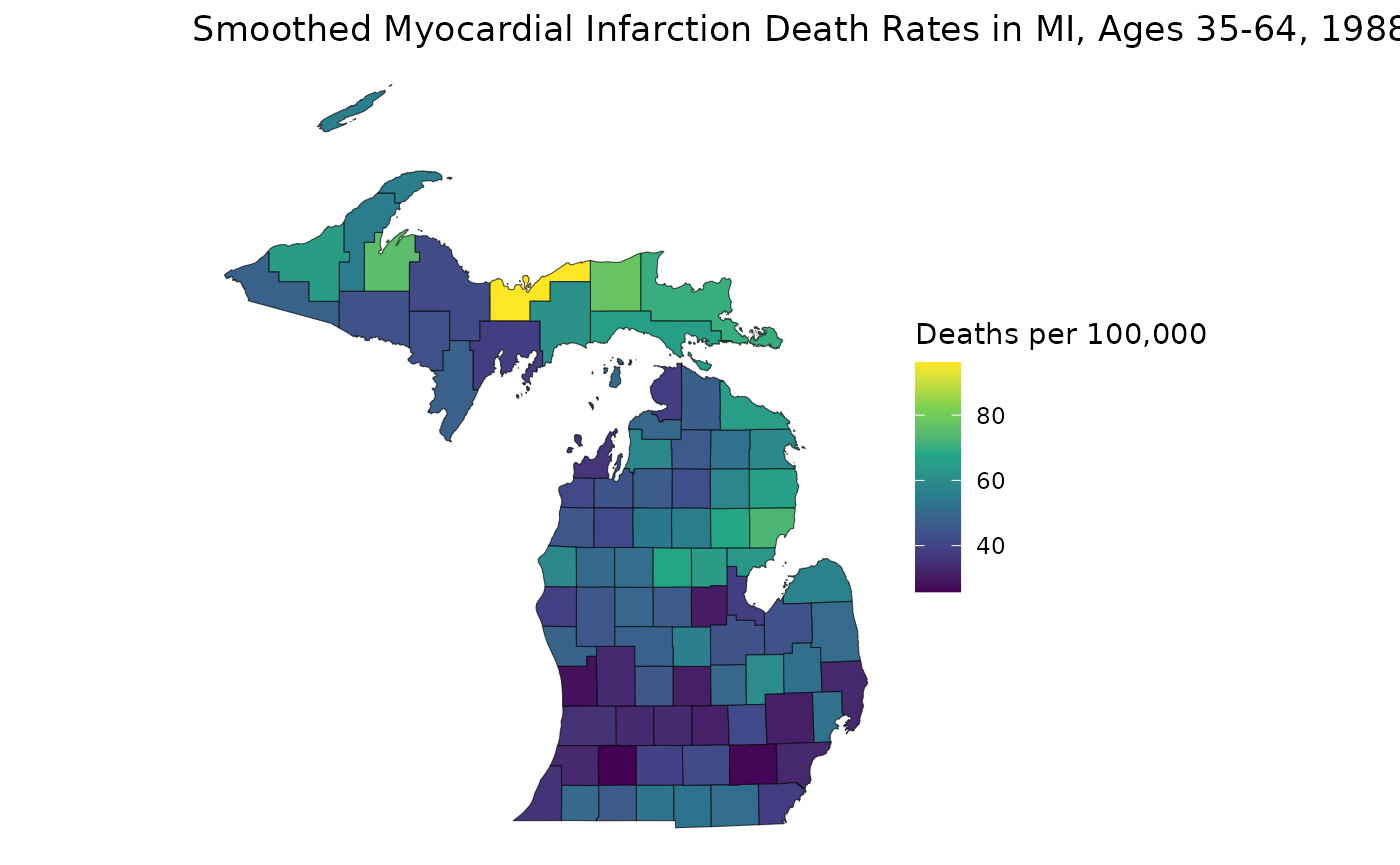

This map helps us see how RSTr smooths rates. First, notice how the range of the two plots are different: the smoothed map has a smaller range because RSTr stabilizes high and low extreme values which are usually caused by low population counts. Also, notice how the transitions between high-rate and low-rate regions are more gradual on the smoothed map. This is a consequence of using neighboring regions to inform and stabilize estimates.

From here, we can get a better idea of how these maps contrast. For example, on the first map, the largest region of interest is the middle portion of the Lower Peninsula (LP), but on the smoothed map, much of this area has attenuated rates. On the flip side, many areas in the Upper Peninsula (UP) have relatively lower rates on the first map, but we can see on the smoothed map that the highest rate in the state is in the UP. The higher-rate areas on the LP are focused around counties on Saginaw Bay in the east, indicating that these areas may require more attention than previously thought. These are the kinds of inferences that can be made using estimates generated by the RSTr package and the main motivation for running this spatiotemporal model.

Closing Thoughts

This vignette introduces you to inputting data into the mstcar() function, extracting estimates with the get_estimates() function, age-standardizing estimates with the age_standardize() function, suppressing estimates with the suppress_estimates() function, and finally making a map with estimates gathered from get_estimates() function. What we’ve discussed here is just scratching the surface of the RSTr package. Other package vignettes will dive deeper into the intricacies of each component of the package. All of these things together will ensure you get the most out of using RSTr.