
06: Calculating Parameter Medians
RSTr-medians.RmdOverview
In the previous vignette, we finally ran our model using
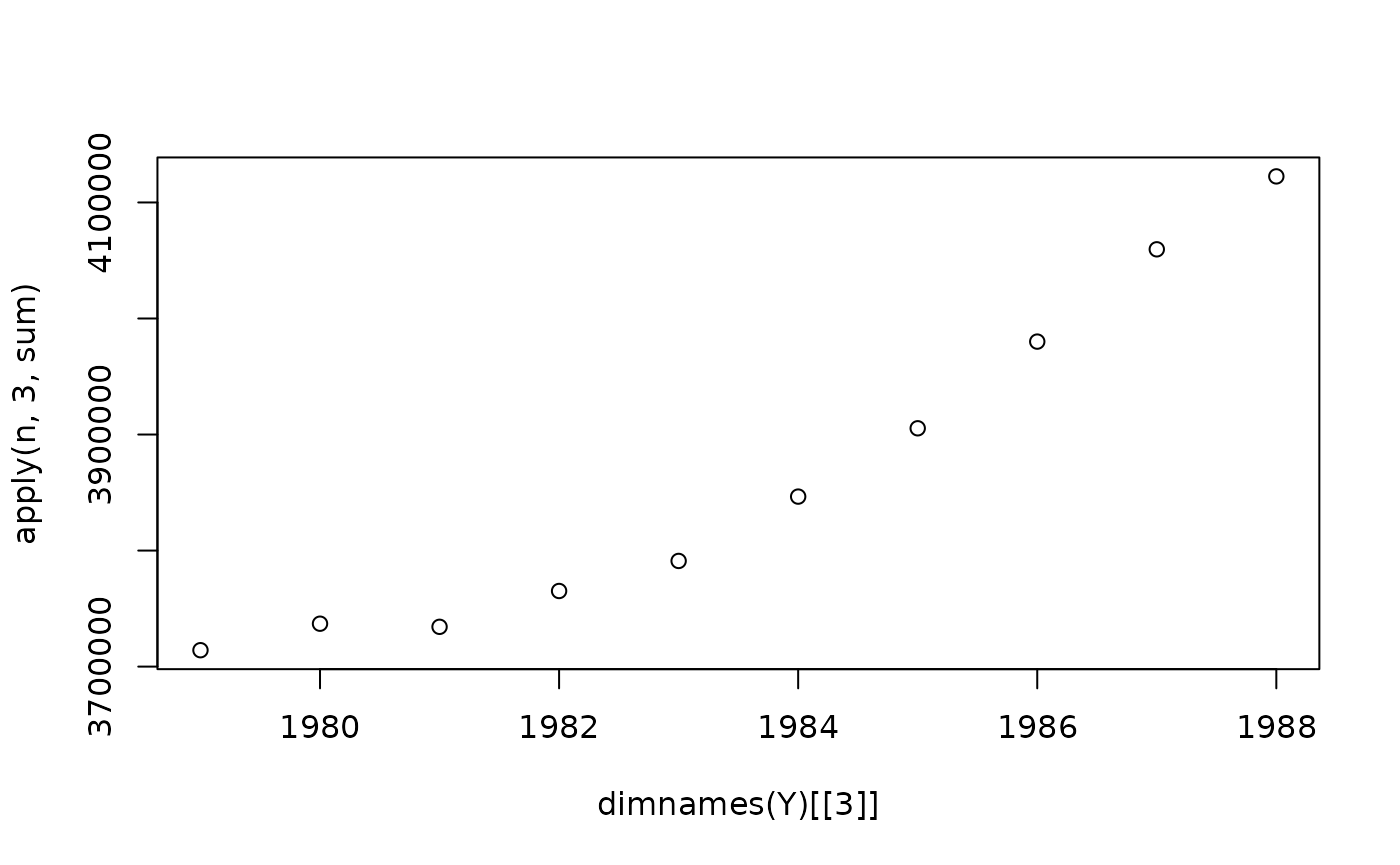
run_sampler(), imported estimates using
load_samples(), age-standardized and year-aggregated our
estimates, and finally did some cursory exploration of large- and
small-population counties in our dataset. Now, we can calculate our
estimates, investigate measures of reliability, and investigate the
implications of our measures of reliability. Note that this process is
identical for all types of models.
The get_medians() function
Previously, we generated age-standardized estimates for
theta based on our example Michigan dataset,
theta.
# from vignette("RSTr-samples")
library(RSTr)
initialize_model(name = "my_test_model", data = miheart, adjacency = miadj)
#> Checking data...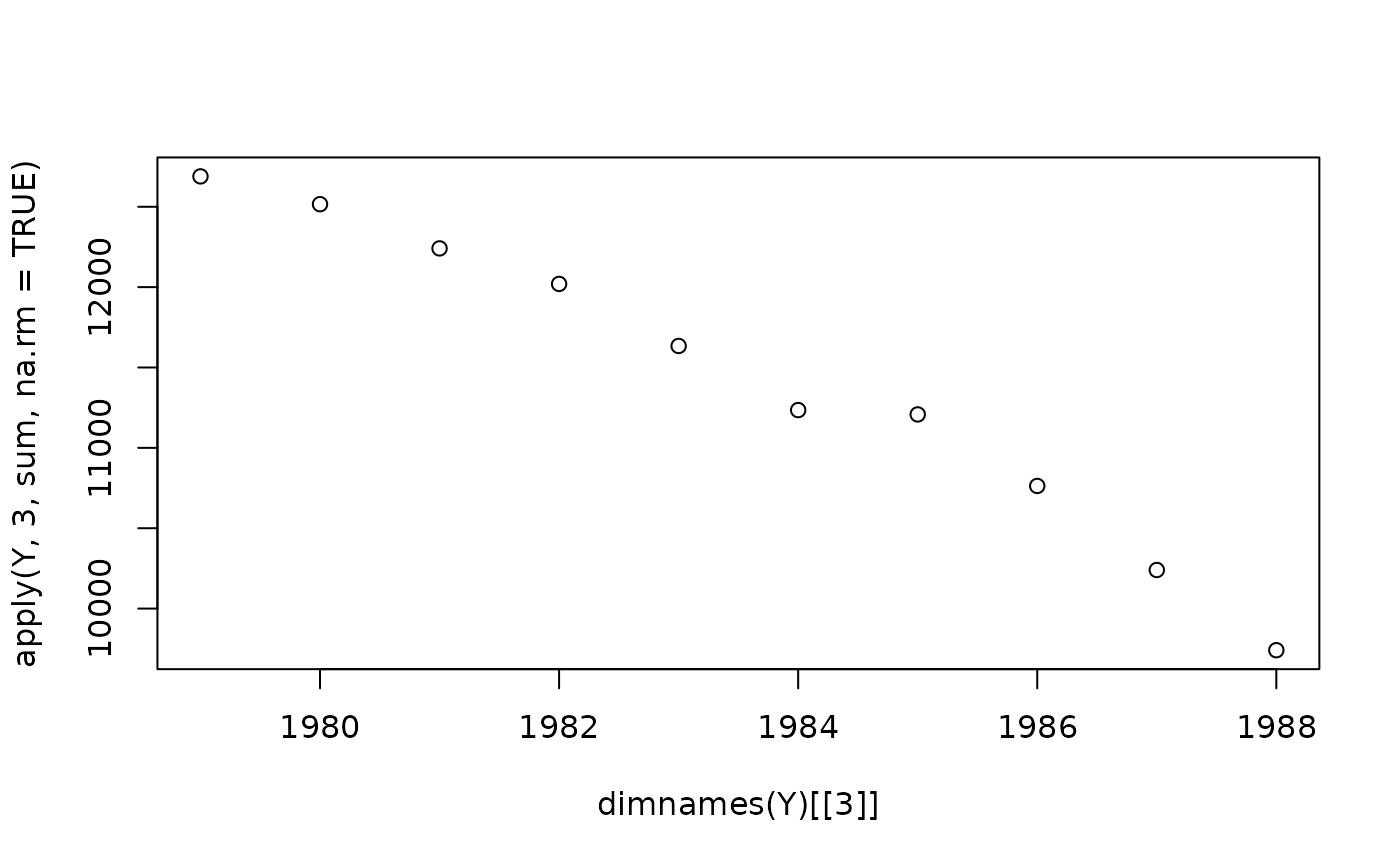
#> Checking spatial data...
#> Checking priors...
#> The following objects were created using defaults in 'priors':theta_sd tau_a tau_b Ag_scale Ag_df G_df rho_a rho_b rho_sd
#> Checking inits...
#> The following objects were created using defaults in 'inits':beta theta Z G rho tau2 Ag
#> Model ready!
run_sampler("my_test_model")
#> Starting sampler on Batch 1at Tue Sep 16 20:24:41
#> Batch 1/60, Progress: |..................................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |..................................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*.................................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*.................................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**................................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**................................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***...............................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***...............................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |****..............................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |****..............................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*****.............................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*****.............................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |******............................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |******............................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*******...........................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*******...........................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |********..........................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |********..........................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*********.........................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*********.........................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**********........................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**********........................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***********.......................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***********.......................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |************......................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |************......................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*************.....................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*************.....................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**************....................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**************....................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***************...................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***************...................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |****************..................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |****************..................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*****************.................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*****************.................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |******************................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |******************................................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*******************...............................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*******************...............................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |********************..............................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |********************..............................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*********************.............................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*********************.............................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**********************............................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**********************............................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***********************...........................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***********************...........................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |************************..........................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |************************..........................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*************************.........................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*************************.........................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**************************........................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**************************........................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***************************.......................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***************************.......................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |****************************......................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |****************************......................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*****************************.....................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*****************************.....................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |******************************....................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |******************************....................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*******************************...................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*******************************...................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |********************************..................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |********************************..................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*********************************.................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*********************************.................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**********************************................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**********************************................| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***********************************...............| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***********************************...............| Elapsed Time: 00:00:00 Batch 1/60, Progress: |************************************..............| Elapsed Time: 00:00:00 Batch 1/60, Progress: |************************************..............| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*************************************.............| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*************************************.............| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**************************************............| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**************************************............| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***************************************...........| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***************************************...........| Elapsed Time: 00:00:00 Batch 1/60, Progress: |****************************************..........| Elapsed Time: 00:00:00 Batch 1/60, Progress: |****************************************..........| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*****************************************.........| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*****************************************.........| Elapsed Time: 00:00:00 Batch 1/60, Progress: |******************************************........| Elapsed Time: 00:00:00 Batch 1/60, Progress: |******************************************........| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*******************************************.......| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*******************************************.......| Elapsed Time: 00:00:00 Batch 1/60, Progress: |********************************************......| Elapsed Time: 00:00:00 Batch 1/60, Progress: |********************************************......| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*********************************************.....| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*********************************************.....| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**********************************************....| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**********************************************....| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***********************************************...| Elapsed Time: 00:00:00 Batch 1/60, Progress: |***********************************************...| Elapsed Time: 00:00:00 Batch 1/60, Progress: |************************************************..| Elapsed Time: 00:00:00 Batch 1/60, Progress: |************************************************..| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*************************************************.| Elapsed Time: 00:00:00 Batch 1/60, Progress: |*************************************************.| Elapsed Time: 00:00:00 Batch 1/60, Progress: |**************************************************| Elapsed Time: 00:00:00 
#> Batch 2/60, Progress: |..................................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |..................................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*.................................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*.................................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**................................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**................................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***...............................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***...............................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |****..............................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |****..............................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*****.............................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*****.............................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |******............................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |******............................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*******...........................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*******...........................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |********..........................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |********..........................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*********.........................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*********.........................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**********........................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**********........................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***********.......................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***********.......................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |************......................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |************......................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*************.....................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*************.....................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**************....................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**************....................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***************...................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***************...................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |****************..................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |****************..................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*****************.................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*****************.................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |******************................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |******************................................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*******************...............................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*******************...............................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |********************..............................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |********************..............................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*********************.............................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*********************.............................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**********************............................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**********************............................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***********************...........................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***********************...........................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |************************..........................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |************************..........................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*************************.........................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*************************.........................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**************************........................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**************************........................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***************************.......................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***************************.......................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |****************************......................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |****************************......................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*****************************.....................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*****************************.....................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |******************************....................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |******************************....................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*******************************...................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*******************************...................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |********************************..................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |********************************..................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*********************************.................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*********************************.................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**********************************................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**********************************................| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***********************************...............| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***********************************...............| Elapsed Time: 00:00:00 Batch 2/60, Progress: |************************************..............| Elapsed Time: 00:00:00 Batch 2/60, Progress: |************************************..............| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*************************************.............| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*************************************.............| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**************************************............| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**************************************............| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***************************************...........| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***************************************...........| Elapsed Time: 00:00:00 Batch 2/60, Progress: |****************************************..........| Elapsed Time: 00:00:00 Batch 2/60, Progress: |****************************************..........| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*****************************************.........| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*****************************************.........| Elapsed Time: 00:00:00 Batch 2/60, Progress: |******************************************........| Elapsed Time: 00:00:00 Batch 2/60, Progress: |******************************************........| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*******************************************.......| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*******************************************.......| Elapsed Time: 00:00:00 Batch 2/60, Progress: |********************************************......| Elapsed Time: 00:00:00 Batch 2/60, Progress: |********************************************......| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*********************************************.....| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*********************************************.....| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**********************************************....| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**********************************************....| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***********************************************...| Elapsed Time: 00:00:00 Batch 2/60, Progress: |***********************************************...| Elapsed Time: 00:00:00 Batch 2/60, Progress: |************************************************..| Elapsed Time: 00:00:00 Batch 2/60, Progress: |************************************************..| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*************************************************.| Elapsed Time: 00:00:00 Batch 2/60, Progress: |*************************************************.| Elapsed Time: 00:00:00 Batch 2/60, Progress: |**************************************************| Elapsed Time: 00:00:00 
#> Batch 3/60, Progress: |..................................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |..................................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*.................................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*.................................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |**................................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |**................................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |***...............................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |***...............................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |****..............................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |****..............................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*****.............................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*****.............................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |******............................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |******............................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*******...........................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*******...........................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |********..........................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |********..........................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*********.........................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*********.........................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |**********........................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |**********........................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |***********.......................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |***********.......................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |************......................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |************......................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*************.....................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |*************.....................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |**************....................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |**************....................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |***************...................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |***************...................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |****************..................................| Elapsed Time: 00:00:00 Batch 3/60, Progress: |****************..................................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*****************.................................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*****************.................................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |******************................................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |******************................................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*******************...............................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*******************...............................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |********************..............................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |********************..............................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*********************.............................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*********************.............................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**********************............................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**********************............................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***********************...........................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***********************...........................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |************************..........................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |************************..........................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*************************.........................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*************************.........................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**************************........................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**************************........................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***************************.......................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***************************.......................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |****************************......................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |****************************......................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*****************************.....................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*****************************.....................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |******************************....................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |******************************....................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*******************************...................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*******************************...................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |********************************..................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |********************************..................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*********************************.................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*********************************.................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**********************************................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**********************************................| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***********************************...............| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***********************************...............| Elapsed Time: 00:00:01 Batch 3/60, Progress: |************************************..............| Elapsed Time: 00:00:01 Batch 3/60, Progress: |************************************..............| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*************************************.............| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*************************************.............| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**************************************............| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**************************************............| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***************************************...........| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***************************************...........| Elapsed Time: 00:00:01 Batch 3/60, Progress: |****************************************..........| Elapsed Time: 00:00:01 Batch 3/60, Progress: |****************************************..........| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*****************************************.........| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*****************************************.........| Elapsed Time: 00:00:01 Batch 3/60, Progress: |******************************************........| Elapsed Time: 00:00:01 Batch 3/60, Progress: |******************************************........| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*******************************************.......| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*******************************************.......| Elapsed Time: 00:00:01 Batch 3/60, Progress: |********************************************......| Elapsed Time: 00:00:01 Batch 3/60, Progress: |********************************************......| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*********************************************.....| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*********************************************.....| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**********************************************....| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**********************************************....| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***********************************************...| Elapsed Time: 00:00:01 Batch 3/60, Progress: |***********************************************...| Elapsed Time: 00:00:01 Batch 3/60, Progress: |************************************************..| Elapsed Time: 00:00:01 Batch 3/60, Progress: |************************************************..| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*************************************************.| Elapsed Time: 00:00:01 Batch 3/60, Progress: |*************************************************.| Elapsed Time: 00:00:01 Batch 3/60, Progress: |**************************************************| Elapsed Time: 00:00:01 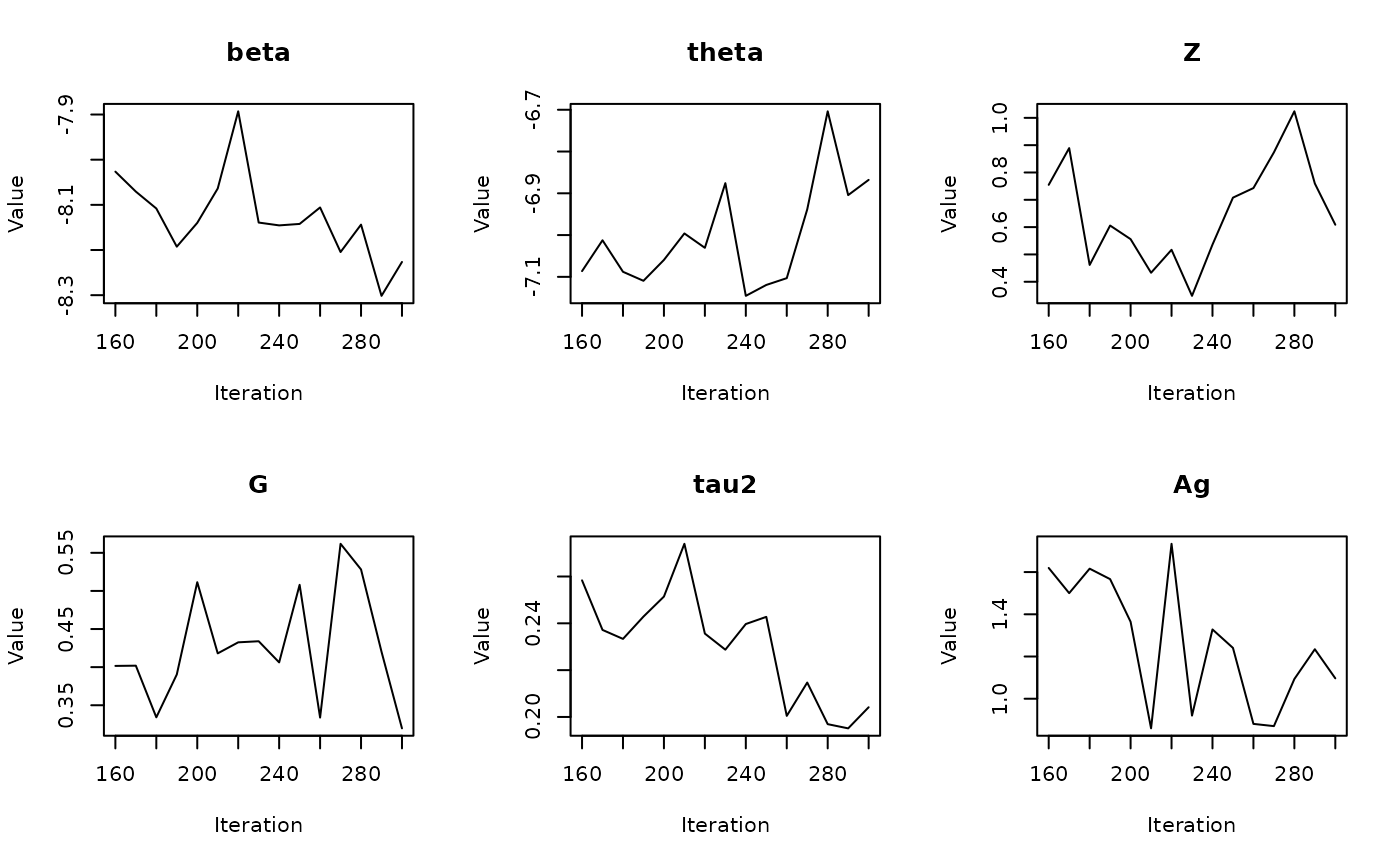
#> Batch 4/60, Progress: |..................................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |..................................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*.................................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*.................................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**................................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**................................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***...............................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***...............................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |****..............................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |****..............................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*****.............................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*****.............................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |******............................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |******............................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*******...........................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*******...........................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |********..........................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |********..........................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*********.........................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*********.........................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**********........................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**********........................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***********.......................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***********.......................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |************......................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |************......................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*************.....................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*************.....................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**************....................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**************....................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***************...................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***************...................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |****************..................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |****************..................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*****************.................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*****************.................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |******************................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |******************................................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*******************...............................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*******************...............................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |********************..............................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |********************..............................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*********************.............................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*********************.............................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**********************............................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**********************............................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***********************...........................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***********************...........................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |************************..........................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |************************..........................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*************************.........................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*************************.........................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**************************........................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**************************........................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***************************.......................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***************************.......................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |****************************......................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |****************************......................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*****************************.....................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*****************************.....................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |******************************....................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |******************************....................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*******************************...................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*******************************...................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |********************************..................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |********************************..................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*********************************.................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*********************************.................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**********************************................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**********************************................| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***********************************...............| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***********************************...............| Elapsed Time: 00:00:01 Batch 4/60, Progress: |************************************..............| Elapsed Time: 00:00:01 Batch 4/60, Progress: |************************************..............| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*************************************.............| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*************************************.............| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**************************************............| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**************************************............| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***************************************...........| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***************************************...........| Elapsed Time: 00:00:01 Batch 4/60, Progress: |****************************************..........| Elapsed Time: 00:00:01 Batch 4/60, Progress: |****************************************..........| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*****************************************.........| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*****************************************.........| Elapsed Time: 00:00:01 Batch 4/60, Progress: |******************************************........| Elapsed Time: 00:00:01 Batch 4/60, Progress: |******************************************........| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*******************************************.......| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*******************************************.......| Elapsed Time: 00:00:01 Batch 4/60, Progress: |********************************************......| Elapsed Time: 00:00:01 Batch 4/60, Progress: |********************************************......| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*********************************************.....| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*********************************************.....| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**********************************************....| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**********************************************....| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***********************************************...| Elapsed Time: 00:00:01 Batch 4/60, Progress: |***********************************************...| Elapsed Time: 00:00:01 Batch 4/60, Progress: |************************************************..| Elapsed Time: 00:00:01 Batch 4/60, Progress: |************************************************..| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*************************************************.| Elapsed Time: 00:00:01 Batch 4/60, Progress: |*************************************************.| Elapsed Time: 00:00:01 Batch 4/60, Progress: |**************************************************| Elapsed Time: 00:00:01 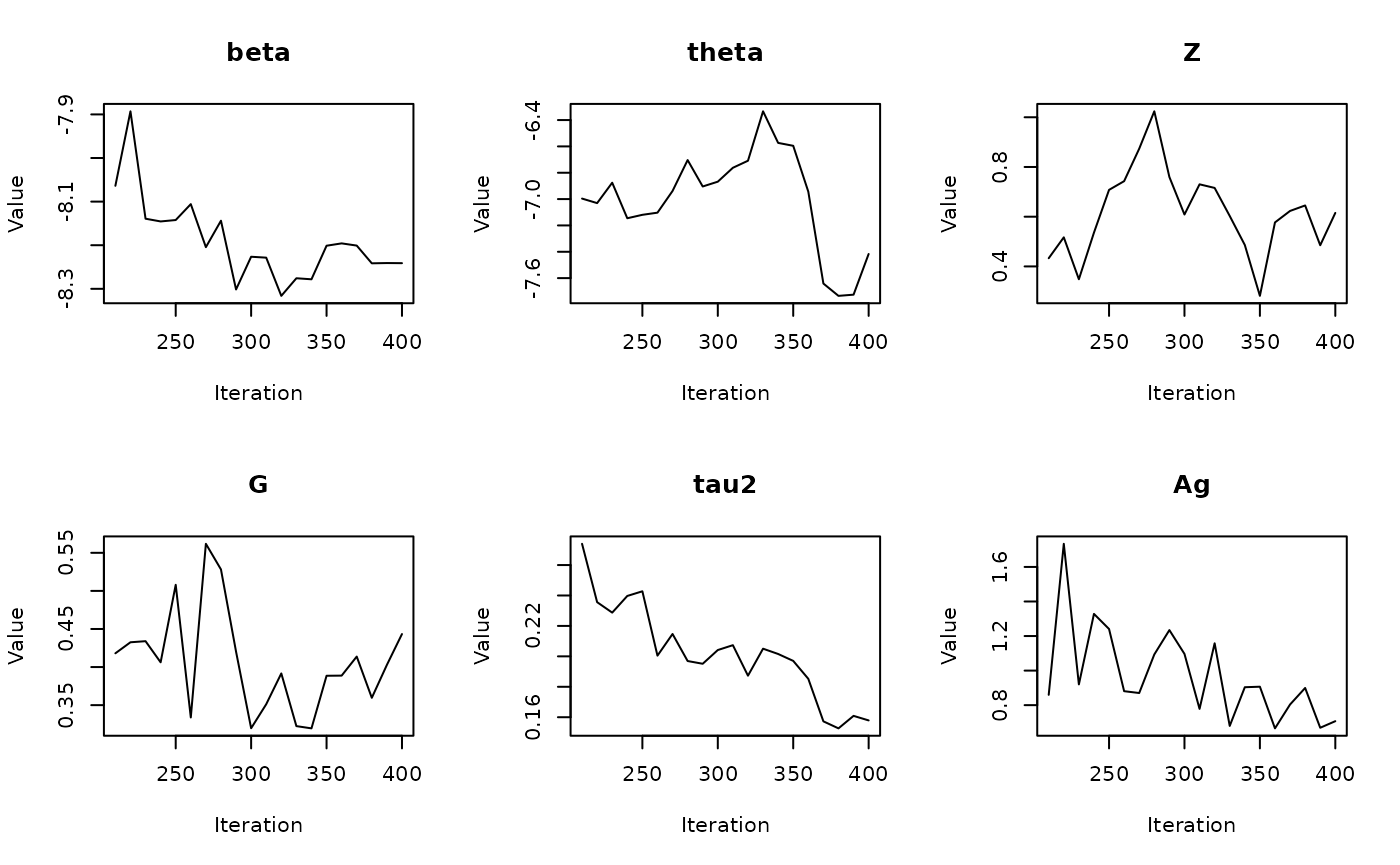
#> Batch 5/60, Progress: |..................................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |..................................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*.................................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*.................................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**................................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**................................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***...............................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***...............................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |****..............................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |****..............................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*****.............................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*****.............................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |******............................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |******............................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*******...........................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*******...........................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |********..........................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |********..........................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*********.........................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*********.........................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**********........................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**********........................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***********.......................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***********.......................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |************......................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |************......................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*************.....................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*************.....................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**************....................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**************....................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***************...................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***************...................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |****************..................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |****************..................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*****************.................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*****************.................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |******************................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |******************................................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*******************...............................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*******************...............................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |********************..............................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |********************..............................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*********************.............................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*********************.............................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**********************............................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**********************............................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***********************...........................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***********************...........................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |************************..........................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |************************..........................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*************************.........................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*************************.........................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**************************........................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**************************........................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***************************.......................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***************************.......................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |****************************......................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |****************************......................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*****************************.....................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*****************************.....................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |******************************....................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |******************************....................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*******************************...................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*******************************...................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |********************************..................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |********************************..................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*********************************.................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*********************************.................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**********************************................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**********************************................| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***********************************...............| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***********************************...............| Elapsed Time: 00:00:01 Batch 5/60, Progress: |************************************..............| Elapsed Time: 00:00:01 Batch 5/60, Progress: |************************************..............| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*************************************.............| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*************************************.............| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**************************************............| Elapsed Time: 00:00:01 Batch 5/60, Progress: |**************************************............| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***************************************...........| Elapsed Time: 00:00:01 Batch 5/60, Progress: |***************************************...........| Elapsed Time: 00:00:01 Batch 5/60, Progress: |****************************************..........| Elapsed Time: 00:00:01 Batch 5/60, Progress: |****************************************..........| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*****************************************.........| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*****************************************.........| Elapsed Time: 00:00:01 Batch 5/60, Progress: |******************************************........| Elapsed Time: 00:00:01 Batch 5/60, Progress: |******************************************........| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*******************************************.......| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*******************************************.......| Elapsed Time: 00:00:01 Batch 5/60, Progress: |********************************************......| Elapsed Time: 00:00:01 Batch 5/60, Progress: |********************************************......| Elapsed Time: 00:00:01 Batch 5/60, Progress: |*********************************************.....| Elapsed Time: 00:00:02 Batch 5/60, Progress: |*********************************************.....| Elapsed Time: 00:00:02 Batch 5/60, Progress: |**********************************************....| Elapsed Time: 00:00:02 Batch 5/60, Progress: |**********************************************....| Elapsed Time: 00:00:02 Batch 5/60, Progress: |***********************************************...| Elapsed Time: 00:00:02 Batch 5/60, Progress: |***********************************************...| Elapsed Time: 00:00:02 Batch 5/60, Progress: |************************************************..| Elapsed Time: 00:00:02 Batch 5/60, Progress: |************************************************..| Elapsed Time: 00:00:02 Batch 5/60, Progress: |*************************************************.| Elapsed Time: 00:00:02 Batch 5/60, Progress: |*************************************************.| Elapsed Time: 00:00:02 Batch 5/60, Progress: |**************************************************| Elapsed Time: 00:00:02 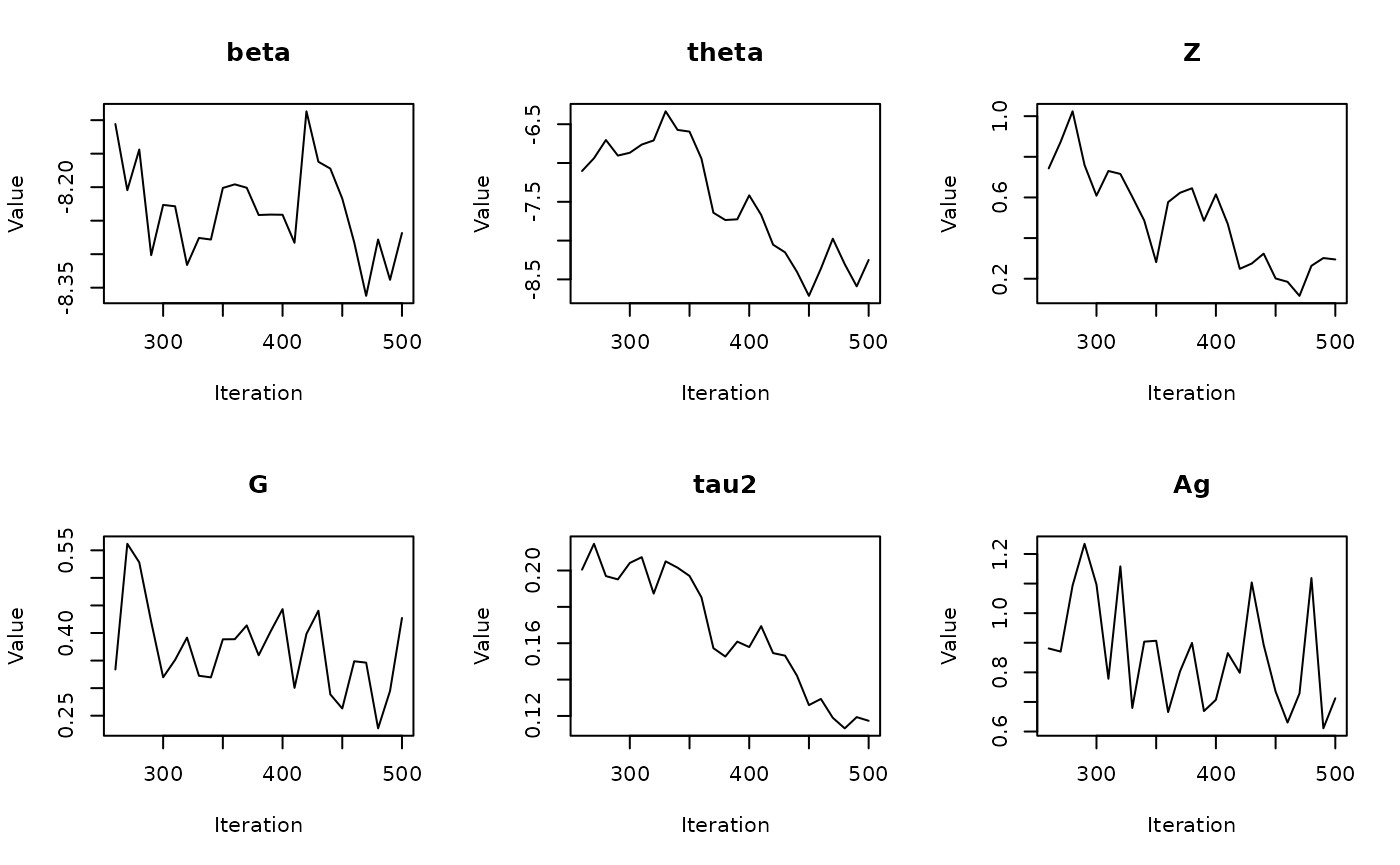
#> Batch 6/60, Progress: |..................................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |..................................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*.................................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*.................................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**................................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**................................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***...............................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***...............................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |****..............................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |****..............................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*****.............................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*****.............................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |******............................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |******............................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*******...........................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*******...........................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |********..........................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |********..........................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*********.........................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*********.........................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**********........................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**********........................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***********.......................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***********.......................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |************......................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |************......................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*************.....................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*************.....................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**************....................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**************....................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***************...................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***************...................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |****************..................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |****************..................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*****************.................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*****************.................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |******************................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |******************................................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*******************...............................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*******************...............................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |********************..............................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |********************..............................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*********************.............................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*********************.............................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**********************............................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**********************............................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***********************...........................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***********************...........................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |************************..........................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |************************..........................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*************************.........................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*************************.........................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**************************........................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**************************........................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***************************.......................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***************************.......................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |****************************......................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |****************************......................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*****************************.....................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*****************************.....................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |******************************....................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |******************************....................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*******************************...................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*******************************...................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |********************************..................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |********************************..................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*********************************.................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*********************************.................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**********************************................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**********************************................| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***********************************...............| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***********************************...............| Elapsed Time: 00:00:02 Batch 6/60, Progress: |************************************..............| Elapsed Time: 00:00:02 Batch 6/60, Progress: |************************************..............| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*************************************.............| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*************************************.............| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**************************************............| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**************************************............| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***************************************...........| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***************************************...........| Elapsed Time: 00:00:02 Batch 6/60, Progress: |****************************************..........| Elapsed Time: 00:00:02 Batch 6/60, Progress: |****************************************..........| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*****************************************.........| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*****************************************.........| Elapsed Time: 00:00:02 Batch 6/60, Progress: |******************************************........| Elapsed Time: 00:00:02 Batch 6/60, Progress: |******************************************........| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*******************************************.......| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*******************************************.......| Elapsed Time: 00:00:02 Batch 6/60, Progress: |********************************************......| Elapsed Time: 00:00:02 Batch 6/60, Progress: |********************************************......| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*********************************************.....| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*********************************************.....| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**********************************************....| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**********************************************....| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***********************************************...| Elapsed Time: 00:00:02 Batch 6/60, Progress: |***********************************************...| Elapsed Time: 00:00:02 Batch 6/60, Progress: |************************************************..| Elapsed Time: 00:00:02 Batch 6/60, Progress: |************************************************..| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*************************************************.| Elapsed Time: 00:00:02 Batch 6/60, Progress: |*************************************************.| Elapsed Time: 00:00:02 Batch 6/60, Progress: |**************************************************| Elapsed Time: 00:00:02 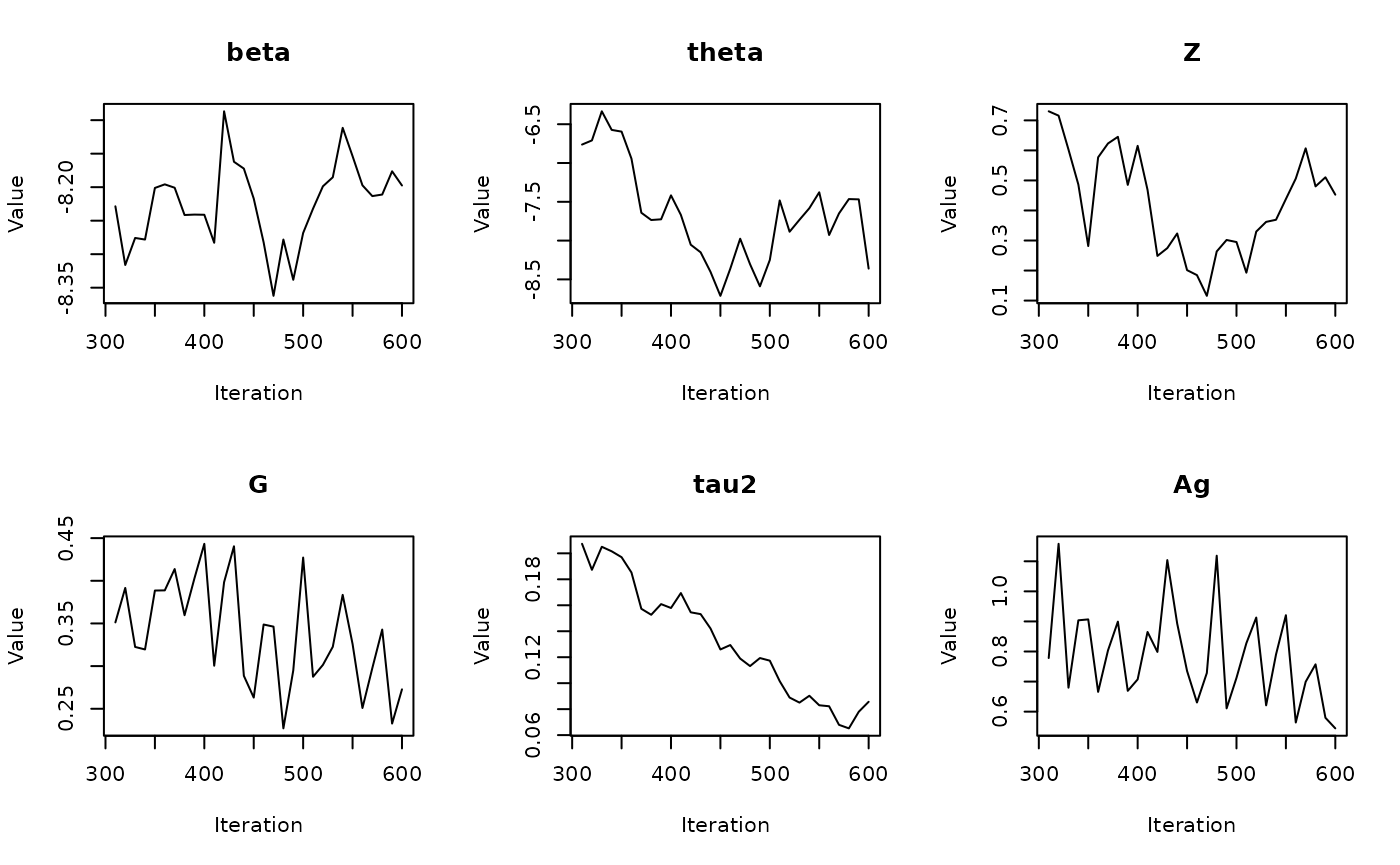
#> Batch 7/60, Progress: |..................................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |..................................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*.................................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*.................................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**................................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**................................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***...............................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***...............................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |****..............................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |****..............................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*****.............................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*****.............................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |******............................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |******............................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*******...........................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*******...........................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |********..........................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |********..........................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*********.........................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*********.........................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**********........................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**********........................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***********.......................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***********.......................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |************......................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |************......................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*************.....................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*************.....................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**************....................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**************....................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***************...................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***************...................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |****************..................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |****************..................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*****************.................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*****************.................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |******************................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |******************................................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*******************...............................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*******************...............................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |********************..............................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |********************..............................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*********************.............................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*********************.............................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**********************............................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**********************............................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***********************...........................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***********************...........................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |************************..........................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |************************..........................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*************************.........................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*************************.........................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**************************........................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**************************........................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***************************.......................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***************************.......................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |****************************......................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |****************************......................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*****************************.....................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*****************************.....................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |******************************....................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |******************************....................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*******************************...................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*******************************...................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |********************************..................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |********************************..................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*********************************.................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*********************************.................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**********************************................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**********************************................| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***********************************...............| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***********************************...............| Elapsed Time: 00:00:02 Batch 7/60, Progress: |************************************..............| Elapsed Time: 00:00:02 Batch 7/60, Progress: |************************************..............| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*************************************.............| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*************************************.............| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**************************************............| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**************************************............| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***************************************...........| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***************************************...........| Elapsed Time: 00:00:02 Batch 7/60, Progress: |****************************************..........| Elapsed Time: 00:00:02 Batch 7/60, Progress: |****************************************..........| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*****************************************.........| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*****************************************.........| Elapsed Time: 00:00:02 Batch 7/60, Progress: |******************************************........| Elapsed Time: 00:00:02 Batch 7/60, Progress: |******************************************........| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*******************************************.......| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*******************************************.......| Elapsed Time: 00:00:02 Batch 7/60, Progress: |********************************************......| Elapsed Time: 00:00:02 Batch 7/60, Progress: |********************************************......| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*********************************************.....| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*********************************************.....| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**********************************************....| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**********************************************....| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***********************************************...| Elapsed Time: 00:00:02 Batch 7/60, Progress: |***********************************************...| Elapsed Time: 00:00:02 Batch 7/60, Progress: |************************************************..| Elapsed Time: 00:00:02 Batch 7/60, Progress: |************************************************..| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*************************************************.| Elapsed Time: 00:00:02 Batch 7/60, Progress: |*************************************************.| Elapsed Time: 00:00:02 Batch 7/60, Progress: |**************************************************| Elapsed Time: 00:00:02 
#> Batch 8/60, Progress: |..................................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |..................................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |*.................................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |*.................................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |**................................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |**................................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |***...............................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |***...............................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |****..............................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |****..............................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |*****.............................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |*****.............................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |******............................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |******............................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |*******...........................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |*******...........................................| Elapsed Time: 00:00:02 Batch 8/60, Progress: |********..........................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |********..........................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*********.........................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*********.........................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**********........................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**********........................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***********.......................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***********.......................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |************......................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |************......................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*************.....................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*************.....................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**************....................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**************....................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***************...................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***************...................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |****************..................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |****************..................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*****************.................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*****************.................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |******************................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |******************................................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*******************...............................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*******************...............................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |********************..............................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |********************..............................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*********************.............................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*********************.............................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**********************............................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**********************............................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***********************...........................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***********************...........................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |************************..........................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |************************..........................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*************************.........................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*************************.........................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**************************........................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**************************........................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***************************.......................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***************************.......................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |****************************......................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |****************************......................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*****************************.....................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*****************************.....................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |******************************....................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |******************************....................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*******************************...................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*******************************...................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |********************************..................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |********************************..................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*********************************.................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*********************************.................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**********************************................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**********************************................| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***********************************...............| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***********************************...............| Elapsed Time: 00:00:03 Batch 8/60, Progress: |************************************..............| Elapsed Time: 00:00:03 Batch 8/60, Progress: |************************************..............| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*************************************.............| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*************************************.............| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**************************************............| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**************************************............| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***************************************...........| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***************************************...........| Elapsed Time: 00:00:03 Batch 8/60, Progress: |****************************************..........| Elapsed Time: 00:00:03 Batch 8/60, Progress: |****************************************..........| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*****************************************.........| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*****************************************.........| Elapsed Time: 00:00:03 Batch 8/60, Progress: |******************************************........| Elapsed Time: 00:00:03 Batch 8/60, Progress: |******************************************........| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*******************************************.......| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*******************************************.......| Elapsed Time: 00:00:03 Batch 8/60, Progress: |********************************************......| Elapsed Time: 00:00:03 Batch 8/60, Progress: |********************************************......| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*********************************************.....| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*********************************************.....| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**********************************************....| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**********************************************....| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***********************************************...| Elapsed Time: 00:00:03 Batch 8/60, Progress: |***********************************************...| Elapsed Time: 00:00:03 Batch 8/60, Progress: |************************************************..| Elapsed Time: 00:00:03 Batch 8/60, Progress: |************************************************..| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*************************************************.| Elapsed Time: 00:00:03 Batch 8/60, Progress: |*************************************************.| Elapsed Time: 00:00:03 Batch 8/60, Progress: |**************************************************| Elapsed Time: 00:00:03 
#> Batch 9/60, Progress: |..................................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |..................................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*.................................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*.................................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**................................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**................................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***...............................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***...............................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |****..............................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |****..............................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*****.............................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*****.............................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |******............................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |******............................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*******...........................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*******...........................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |********..........................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |********..........................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*********.........................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*********.........................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**********........................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**********........................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***********.......................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***********.......................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |************......................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |************......................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*************.....................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*************.....................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**************....................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**************....................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***************...................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***************...................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |****************..................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |****************..................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*****************.................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*****************.................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |******************................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |******************................................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*******************...............................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*******************...............................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |********************..............................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |********************..............................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*********************.............................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*********************.............................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**********************............................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**********************............................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***********************...........................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***********************...........................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |************************..........................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |************************..........................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*************************.........................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*************************.........................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**************************........................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**************************........................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***************************.......................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***************************.......................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |****************************......................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |****************************......................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*****************************.....................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*****************************.....................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |******************************....................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |******************************....................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*******************************...................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*******************************...................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |********************************..................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |********************************..................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*********************************.................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*********************************.................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**********************************................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**********************************................| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***********************************...............| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***********************************...............| Elapsed Time: 00:00:03 Batch 9/60, Progress: |************************************..............| Elapsed Time: 00:00:03 Batch 9/60, Progress: |************************************..............| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*************************************.............| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*************************************.............| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**************************************............| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**************************************............| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***************************************...........| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***************************************...........| Elapsed Time: 00:00:03 Batch 9/60, Progress: |****************************************..........| Elapsed Time: 00:00:03 Batch 9/60, Progress: |****************************************..........| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*****************************************.........| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*****************************************.........| Elapsed Time: 00:00:03 Batch 9/60, Progress: |******************************************........| Elapsed Time: 00:00:03 Batch 9/60, Progress: |******************************************........| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*******************************************.......| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*******************************************.......| Elapsed Time: 00:00:03 Batch 9/60, Progress: |********************************************......| Elapsed Time: 00:00:03 Batch 9/60, Progress: |********************************************......| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*********************************************.....| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*********************************************.....| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**********************************************....| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**********************************************....| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***********************************************...| Elapsed Time: 00:00:03 Batch 9/60, Progress: |***********************************************...| Elapsed Time: 00:00:03 Batch 9/60, Progress: |************************************************..| Elapsed Time: 00:00:03 Batch 9/60, Progress: |************************************************..| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*************************************************.| Elapsed Time: 00:00:03 Batch 9/60, Progress: |*************************************************.| Elapsed Time: 00:00:03 Batch 9/60, Progress: |**************************************************| Elapsed Time: 00:00:03 
#> Batch 10/60, Progress: |..................................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |..................................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*.................................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*.................................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**................................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**................................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***...............................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***...............................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |****..............................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |****..............................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*****.............................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*****.............................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |******............................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |******............................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*******...........................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*******...........................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |********..........................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |********..........................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*********.........................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*********.........................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**********........................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**********........................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***********.......................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***********.......................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |************......................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |************......................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*************.....................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*************.....................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**************....................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**************....................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***************...................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***************...................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |****************..................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |****************..................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*****************.................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*****************.................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |******************................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |******************................................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*******************...............................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*******************...............................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |********************..............................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |********************..............................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*********************.............................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*********************.............................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**********************............................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**********************............................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***********************...........................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***********************...........................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |************************..........................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |************************..........................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*************************.........................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*************************.........................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**************************........................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**************************........................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***************************.......................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***************************.......................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |****************************......................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |****************************......................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*****************************.....................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*****************************.....................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |******************************....................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |******************************....................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*******************************...................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*******************************...................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |********************************..................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |********************************..................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*********************************.................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*********************************.................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**********************************................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**********************************................| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***********************************...............| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***********************************...............| Elapsed Time: 00:00:03 Batch 10/60, Progress: |************************************..............| Elapsed Time: 00:00:03 Batch 10/60, Progress: |************************************..............| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*************************************.............| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*************************************.............| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**************************************............| Elapsed Time: 00:00:03 Batch 10/60, Progress: |**************************************............| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***************************************...........| Elapsed Time: 00:00:03 Batch 10/60, Progress: |***************************************...........| Elapsed Time: 00:00:03 Batch 10/60, Progress: |****************************************..........| Elapsed Time: 00:00:03 Batch 10/60, Progress: |****************************************..........| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*****************************************.........| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*****************************************.........| Elapsed Time: 00:00:03 Batch 10/60, Progress: |******************************************........| Elapsed Time: 00:00:03 Batch 10/60, Progress: |******************************************........| Elapsed Time: 00:00:03 Batch 10/60, Progress: |*******************************************.......| Elapsed Time: 00:00:04 Batch 10/60, Progress: |*******************************************.......| Elapsed Time: 00:00:04 Batch 10/60, Progress: |********************************************......| Elapsed Time: 00:00:04 Batch 10/60, Progress: |********************************************......| Elapsed Time: 00:00:04 Batch 10/60, Progress: |*********************************************.....| Elapsed Time: 00:00:04 Batch 10/60, Progress: |*********************************************.....| Elapsed Time: 00:00:04 Batch 10/60, Progress: |**********************************************....| Elapsed Time: 00:00:04 Batch 10/60, Progress: |**********************************************....| Elapsed Time: 00:00:04 Batch 10/60, Progress: |***********************************************...| Elapsed Time: 00:00:04 Batch 10/60, Progress: |***********************************************...| Elapsed Time: 00:00:04 Batch 10/60, Progress: |************************************************..| Elapsed Time: 00:00:04 Batch 10/60, Progress: |************************************************..| Elapsed Time: 00:00:04 Batch 10/60, Progress: |*************************************************.| Elapsed Time: 00:00:04 Batch 10/60, Progress: |*************************************************.| Elapsed Time: 00:00:04 Batch 10/60, Progress: |**************************************************| Elapsed Time: 00:00:04 
#> Batch 11/60, Progress: |..................................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |..................................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*.................................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*.................................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**................................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**................................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***...............................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***...............................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |****..............................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |****..............................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*****.............................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*****.............................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |******............................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |******............................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*******...........................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*******...........................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |********..........................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |********..........................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*********.........................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*********.........................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**********........................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**********........................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***********.......................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***********.......................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |************......................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |************......................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*************.....................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*************.....................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**************....................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**************....................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***************...................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***************...................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |****************..................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |****************..................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*****************.................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*****************.................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |******************................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |******************................................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*******************...............................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*******************...............................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |********************..............................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |********************..............................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*********************.............................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*********************.............................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**********************............................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**********************............................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***********************...........................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***********************...........................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |************************..........................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |************************..........................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*************************.........................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*************************.........................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**************************........................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**************************........................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***************************.......................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***************************.......................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |****************************......................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |****************************......................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*****************************.....................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*****************************.....................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |******************************....................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |******************************....................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*******************************...................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*******************************...................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |********************************..................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |********************************..................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*********************************.................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*********************************.................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**********************************................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**********************************................| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***********************************...............| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***********************************...............| Elapsed Time: 00:00:04 Batch 11/60, Progress: |************************************..............| Elapsed Time: 00:00:04 Batch 11/60, Progress: |************************************..............| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*************************************.............| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*************************************.............| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**************************************............| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**************************************............| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***************************************...........| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***************************************...........| Elapsed Time: 00:00:04 Batch 11/60, Progress: |****************************************..........| Elapsed Time: 00:00:04 Batch 11/60, Progress: |****************************************..........| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*****************************************.........| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*****************************************.........| Elapsed Time: 00:00:04 Batch 11/60, Progress: |******************************************........| Elapsed Time: 00:00:04 Batch 11/60, Progress: |******************************************........| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*******************************************.......| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*******************************************.......| Elapsed Time: 00:00:04 Batch 11/60, Progress: |********************************************......| Elapsed Time: 00:00:04 Batch 11/60, Progress: |********************************************......| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*********************************************.....| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*********************************************.....| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**********************************************....| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**********************************************....| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***********************************************...| Elapsed Time: 00:00:04 Batch 11/60, Progress: |***********************************************...| Elapsed Time: 00:00:04 Batch 11/60, Progress: |************************************************..| Elapsed Time: 00:00:04 Batch 11/60, Progress: |************************************************..| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*************************************************.| Elapsed Time: 00:00:04 Batch 11/60, Progress: |*************************************************.| Elapsed Time: 00:00:04 Batch 11/60, Progress: |**************************************************| Elapsed Time: 00:00:04 
#> Batch 12/60, Progress: |..................................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |..................................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*.................................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*.................................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**................................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**................................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***...............................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***...............................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |****..............................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |****..............................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*****.............................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*****.............................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |******............................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |******............................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*******...........................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*******...........................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |********..........................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |********..........................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*********.........................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*********.........................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**********........................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**********........................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***********.......................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***********.......................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |************......................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |************......................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*************.....................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*************.....................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**************....................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**************....................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***************...................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***************...................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |****************..................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |****************..................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*****************.................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*****************.................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |******************................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |******************................................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*******************...............................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*******************...............................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |********************..............................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |********************..............................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*********************.............................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*********************.............................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**********************............................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**********************............................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***********************...........................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***********************...........................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |************************..........................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |************************..........................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*************************.........................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*************************.........................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**************************........................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**************************........................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***************************.......................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***************************.......................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |****************************......................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |****************************......................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*****************************.....................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*****************************.....................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |******************************....................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |******************************....................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*******************************...................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*******************************...................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |********************************..................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |********************************..................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*********************************.................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*********************************.................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**********************************................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**********************************................| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***********************************...............| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***********************************...............| Elapsed Time: 00:00:04 Batch 12/60, Progress: |************************************..............| Elapsed Time: 00:00:04 Batch 12/60, Progress: |************************************..............| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*************************************.............| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*************************************.............| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**************************************............| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**************************************............| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***************************************...........| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***************************************...........| Elapsed Time: 00:00:04 Batch 12/60, Progress: |****************************************..........| Elapsed Time: 00:00:04 Batch 12/60, Progress: |****************************************..........| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*****************************************.........| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*****************************************.........| Elapsed Time: 00:00:04 Batch 12/60, Progress: |******************************************........| Elapsed Time: 00:00:04 Batch 12/60, Progress: |******************************************........| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*******************************************.......| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*******************************************.......| Elapsed Time: 00:00:04 Batch 12/60, Progress: |********************************************......| Elapsed Time: 00:00:04 Batch 12/60, Progress: |********************************************......| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*********************************************.....| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*********************************************.....| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**********************************************....| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**********************************************....| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***********************************************...| Elapsed Time: 00:00:04 Batch 12/60, Progress: |***********************************************...| Elapsed Time: 00:00:04 Batch 12/60, Progress: |************************************************..| Elapsed Time: 00:00:04 Batch 12/60, Progress: |************************************************..| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*************************************************.| Elapsed Time: 00:00:04 Batch 12/60, Progress: |*************************************************.| Elapsed Time: 00:00:04 Batch 12/60, Progress: |**************************************************| Elapsed Time: 00:00:04 
#> Batch 13/60, Progress: |..................................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |..................................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |*.................................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |*.................................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |**................................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |**................................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |***...............................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |***...............................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |****..............................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |****..............................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |*****.............................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |*****.............................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |******............................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |******............................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |*******...........................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |*******...........................................| Elapsed Time: 00:00:04 Batch 13/60, Progress: |********..........................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |********..........................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*********.........................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*********.........................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**********........................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**********........................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***********.......................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***********.......................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |************......................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |************......................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*************.....................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*************.....................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**************....................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**************....................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***************...................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***************...................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |****************..................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |****************..................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*****************.................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*****************.................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |******************................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |******************................................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*******************...............................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*******************...............................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |********************..............................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |********************..............................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*********************.............................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*********************.............................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**********************............................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**********************............................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***********************...........................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***********************...........................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |************************..........................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |************************..........................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*************************.........................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*************************.........................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**************************........................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**************************........................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***************************.......................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***************************.......................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |****************************......................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |****************************......................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*****************************.....................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*****************************.....................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |******************************....................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |******************************....................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*******************************...................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*******************************...................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |********************************..................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |********************************..................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*********************************.................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*********************************.................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**********************************................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**********************************................| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***********************************...............| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***********************************...............| Elapsed Time: 00:00:05 Batch 13/60, Progress: |************************************..............| Elapsed Time: 00:00:05 Batch 13/60, Progress: |************************************..............| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*************************************.............| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*************************************.............| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**************************************............| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**************************************............| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***************************************...........| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***************************************...........| Elapsed Time: 00:00:05 Batch 13/60, Progress: |****************************************..........| Elapsed Time: 00:00:05 Batch 13/60, Progress: |****************************************..........| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*****************************************.........| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*****************************************.........| Elapsed Time: 00:00:05 Batch 13/60, Progress: |******************************************........| Elapsed Time: 00:00:05 Batch 13/60, Progress: |******************************************........| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*******************************************.......| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*******************************************.......| Elapsed Time: 00:00:05 Batch 13/60, Progress: |********************************************......| Elapsed Time: 00:00:05 Batch 13/60, Progress: |********************************************......| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*********************************************.....| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*********************************************.....| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**********************************************....| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**********************************************....| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***********************************************...| Elapsed Time: 00:00:05 Batch 13/60, Progress: |***********************************************...| Elapsed Time: 00:00:05 Batch 13/60, Progress: |************************************************..| Elapsed Time: 00:00:05 Batch 13/60, Progress: |************************************************..| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*************************************************.| Elapsed Time: 00:00:05 Batch 13/60, Progress: |*************************************************.| Elapsed Time: 00:00:05 Batch 13/60, Progress: |**************************************************| Elapsed Time: 00:00:05 
#> Batch 14/60, Progress: |..................................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |..................................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*.................................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*.................................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**................................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**................................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***...............................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***...............................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |****..............................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |****..............................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*****.............................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*****.............................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |******............................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |******............................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*******...........................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*******...........................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |********..........................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |********..........................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*********.........................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*********.........................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**********........................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**********........................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***********.......................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***********.......................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |************......................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |************......................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*************.....................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*************.....................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**************....................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**************....................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***************...................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***************...................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |****************..................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |****************..................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*****************.................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*****************.................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |******************................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |******************................................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*******************...............................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*******************...............................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |********************..............................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |********************..............................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*********************.............................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*********************.............................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**********************............................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**********************............................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***********************...........................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***********************...........................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |************************..........................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |************************..........................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*************************.........................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*************************.........................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**************************........................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**************************........................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***************************.......................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***************************.......................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |****************************......................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |****************************......................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*****************************.....................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*****************************.....................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |******************************....................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |******************************....................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*******************************...................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*******************************...................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |********************************..................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |********************************..................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*********************************.................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*********************************.................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**********************************................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**********************************................| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***********************************...............| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***********************************...............| Elapsed Time: 00:00:05 Batch 14/60, Progress: |************************************..............| Elapsed Time: 00:00:05 Batch 14/60, Progress: |************************************..............| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*************************************.............| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*************************************.............| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**************************************............| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**************************************............| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***************************************...........| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***************************************...........| Elapsed Time: 00:00:05 Batch 14/60, Progress: |****************************************..........| Elapsed Time: 00:00:05 Batch 14/60, Progress: |****************************************..........| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*****************************************.........| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*****************************************.........| Elapsed Time: 00:00:05 Batch 14/60, Progress: |******************************************........| Elapsed Time: 00:00:05 Batch 14/60, Progress: |******************************************........| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*******************************************.......| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*******************************************.......| Elapsed Time: 00:00:05 Batch 14/60, Progress: |********************************************......| Elapsed Time: 00:00:05 Batch 14/60, Progress: |********************************************......| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*********************************************.....| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*********************************************.....| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**********************************************....| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**********************************************....| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***********************************************...| Elapsed Time: 00:00:05 Batch 14/60, Progress: |***********************************************...| Elapsed Time: 00:00:05 Batch 14/60, Progress: |************************************************..| Elapsed Time: 00:00:05 Batch 14/60, Progress: |************************************************..| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*************************************************.| Elapsed Time: 00:00:05 Batch 14/60, Progress: |*************************************************.| Elapsed Time: 00:00:05 Batch 14/60, Progress: |**************************************************| Elapsed Time: 00:00:05 
#> Batch 15/60, Progress: |..................................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |..................................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*.................................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*.................................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**................................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**................................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***...............................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***...............................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |****..............................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |****..............................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*****.............................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*****.............................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |******............................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |******............................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*******...........................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*******...........................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |********..........................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |********..........................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*********.........................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*********.........................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**********........................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**********........................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***********.......................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***********.......................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |************......................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |************......................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*************.....................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*************.....................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**************....................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**************....................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***************...................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***************...................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |****************..................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |****************..................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*****************.................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*****************.................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |******************................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |******************................................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*******************...............................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*******************...............................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |********************..............................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |********************..............................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*********************.............................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*********************.............................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**********************............................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**********************............................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***********************...........................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***********************...........................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |************************..........................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |************************..........................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*************************.........................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*************************.........................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**************************........................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**************************........................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***************************.......................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***************************.......................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |****************************......................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |****************************......................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*****************************.....................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*****************************.....................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |******************************....................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |******************************....................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*******************************...................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*******************************...................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |********************************..................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |********************************..................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*********************************.................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*********************************.................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**********************************................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**********************************................| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***********************************...............| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***********************************...............| Elapsed Time: 00:00:05 Batch 15/60, Progress: |************************************..............| Elapsed Time: 00:00:05 Batch 15/60, Progress: |************************************..............| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*************************************.............| Elapsed Time: 00:00:05 Batch 15/60, Progress: |*************************************.............| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**************************************............| Elapsed Time: 00:00:05 Batch 15/60, Progress: |**************************************............| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***************************************...........| Elapsed Time: 00:00:05 Batch 15/60, Progress: |***************************************...........| Elapsed Time: 00:00:05 Batch 15/60, Progress: |****************************************..........| Elapsed Time: 00:00:05 Batch 15/60, Progress: |****************************************..........| Elapsed Time: 00:00:06 Batch 15/60, Progress: |*****************************************.........| Elapsed Time: 00:00:06 Batch 15/60, Progress: |*****************************************.........| Elapsed Time: 00:00:06 Batch 15/60, Progress: |******************************************........| Elapsed Time: 00:00:06 Batch 15/60, Progress: |******************************************........| Elapsed Time: 00:00:06 Batch 15/60, Progress: |*******************************************.......| Elapsed Time: 00:00:06 Batch 15/60, Progress: |*******************************************.......| Elapsed Time: 00:00:06 Batch 15/60, Progress: |********************************************......| Elapsed Time: 00:00:06 Batch 15/60, Progress: |********************************************......| Elapsed Time: 00:00:06 Batch 15/60, Progress: |*********************************************.....| Elapsed Time: 00:00:06 Batch 15/60, Progress: |*********************************************.....| Elapsed Time: 00:00:06 Batch 15/60, Progress: |**********************************************....| Elapsed Time: 00:00:06 Batch 15/60, Progress: |**********************************************....| Elapsed Time: 00:00:06 Batch 15/60, Progress: |***********************************************...| Elapsed Time: 00:00:06 Batch 15/60, Progress: |***********************************************...| Elapsed Time: 00:00:06 Batch 15/60, Progress: |************************************************..| Elapsed Time: 00:00:06 Batch 15/60, Progress: |************************************************..| Elapsed Time: 00:00:06 Batch 15/60, Progress: |*************************************************.| Elapsed Time: 00:00:06 Batch 15/60, Progress: |*************************************************.| Elapsed Time: 00:00:06 Batch 15/60, Progress: |**************************************************| Elapsed Time: 00:00:06 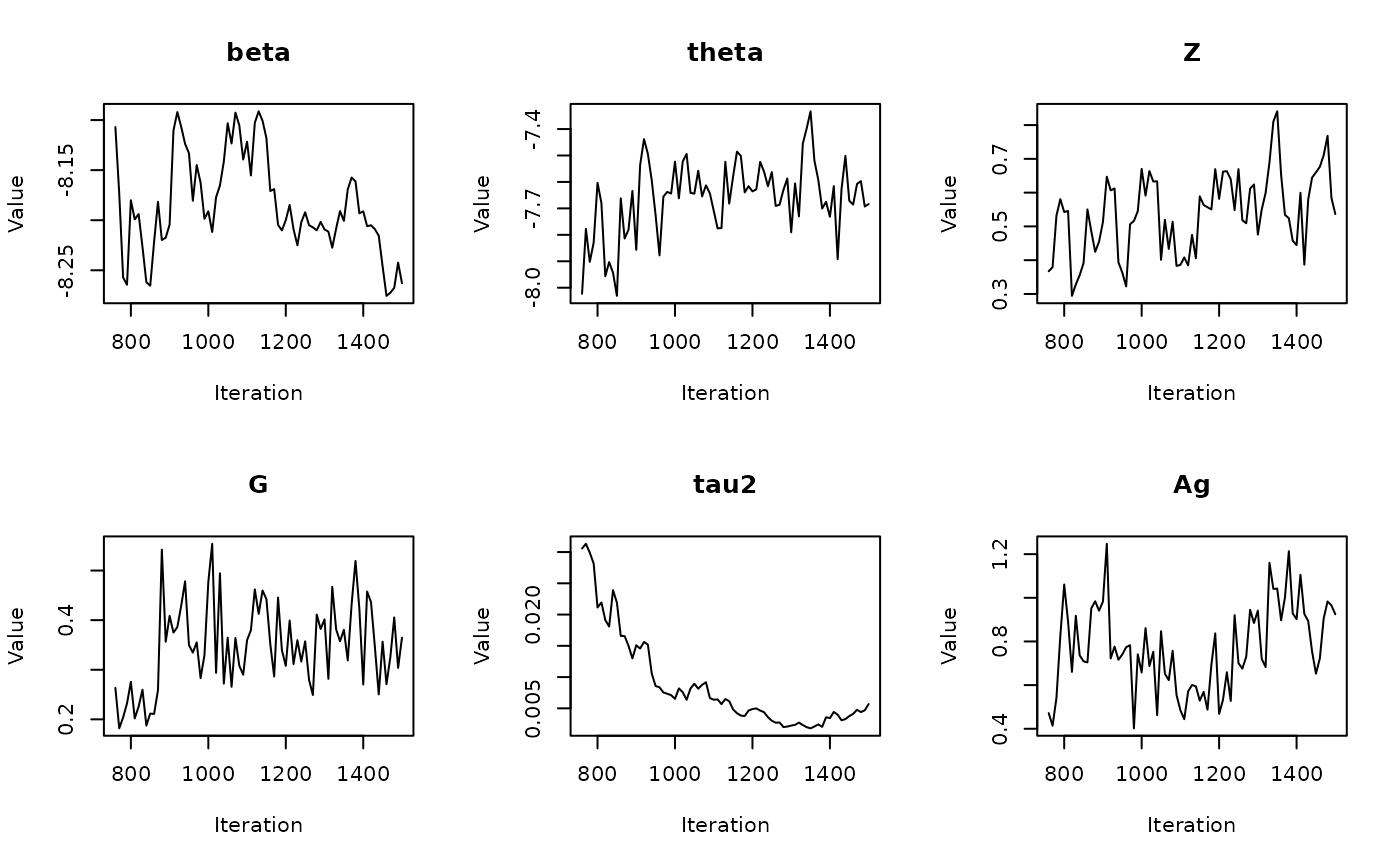
#> Batch 16/60, Progress: |..................................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |..................................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*.................................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*.................................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**................................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**................................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***...............................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***...............................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |****..............................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |****..............................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*****.............................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*****.............................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |******............................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |******............................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*******...........................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*******...........................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |********..........................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |********..........................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*********.........................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*********.........................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**********........................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**********........................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***********.......................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***********.......................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |************......................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |************......................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*************.....................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*************.....................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**************....................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**************....................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***************...................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***************...................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |****************..................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |****************..................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*****************.................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*****************.................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |******************................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |******************................................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*******************...............................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*******************...............................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |********************..............................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |********************..............................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*********************.............................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*********************.............................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**********************............................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**********************............................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***********************...........................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***********************...........................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |************************..........................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |************************..........................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*************************.........................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*************************.........................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**************************........................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**************************........................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***************************.......................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***************************.......................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |****************************......................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |****************************......................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*****************************.....................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*****************************.....................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |******************************....................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |******************************....................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*******************************...................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*******************************...................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |********************************..................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |********************************..................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*********************************.................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*********************************.................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**********************************................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**********************************................| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***********************************...............| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***********************************...............| Elapsed Time: 00:00:06 Batch 16/60, Progress: |************************************..............| Elapsed Time: 00:00:06 Batch 16/60, Progress: |************************************..............| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*************************************.............| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*************************************.............| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**************************************............| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**************************************............| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***************************************...........| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***************************************...........| Elapsed Time: 00:00:06 Batch 16/60, Progress: |****************************************..........| Elapsed Time: 00:00:06 Batch 16/60, Progress: |****************************************..........| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*****************************************.........| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*****************************************.........| Elapsed Time: 00:00:06 Batch 16/60, Progress: |******************************************........| Elapsed Time: 00:00:06 Batch 16/60, Progress: |******************************************........| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*******************************************.......| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*******************************************.......| Elapsed Time: 00:00:06 Batch 16/60, Progress: |********************************************......| Elapsed Time: 00:00:06 Batch 16/60, Progress: |********************************************......| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*********************************************.....| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*********************************************.....| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**********************************************....| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**********************************************....| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***********************************************...| Elapsed Time: 00:00:06 Batch 16/60, Progress: |***********************************************...| Elapsed Time: 00:00:06 Batch 16/60, Progress: |************************************************..| Elapsed Time: 00:00:06 Batch 16/60, Progress: |************************************************..| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*************************************************.| Elapsed Time: 00:00:06 Batch 16/60, Progress: |*************************************************.| Elapsed Time: 00:00:06 Batch 16/60, Progress: |**************************************************| Elapsed Time: 00:00:06 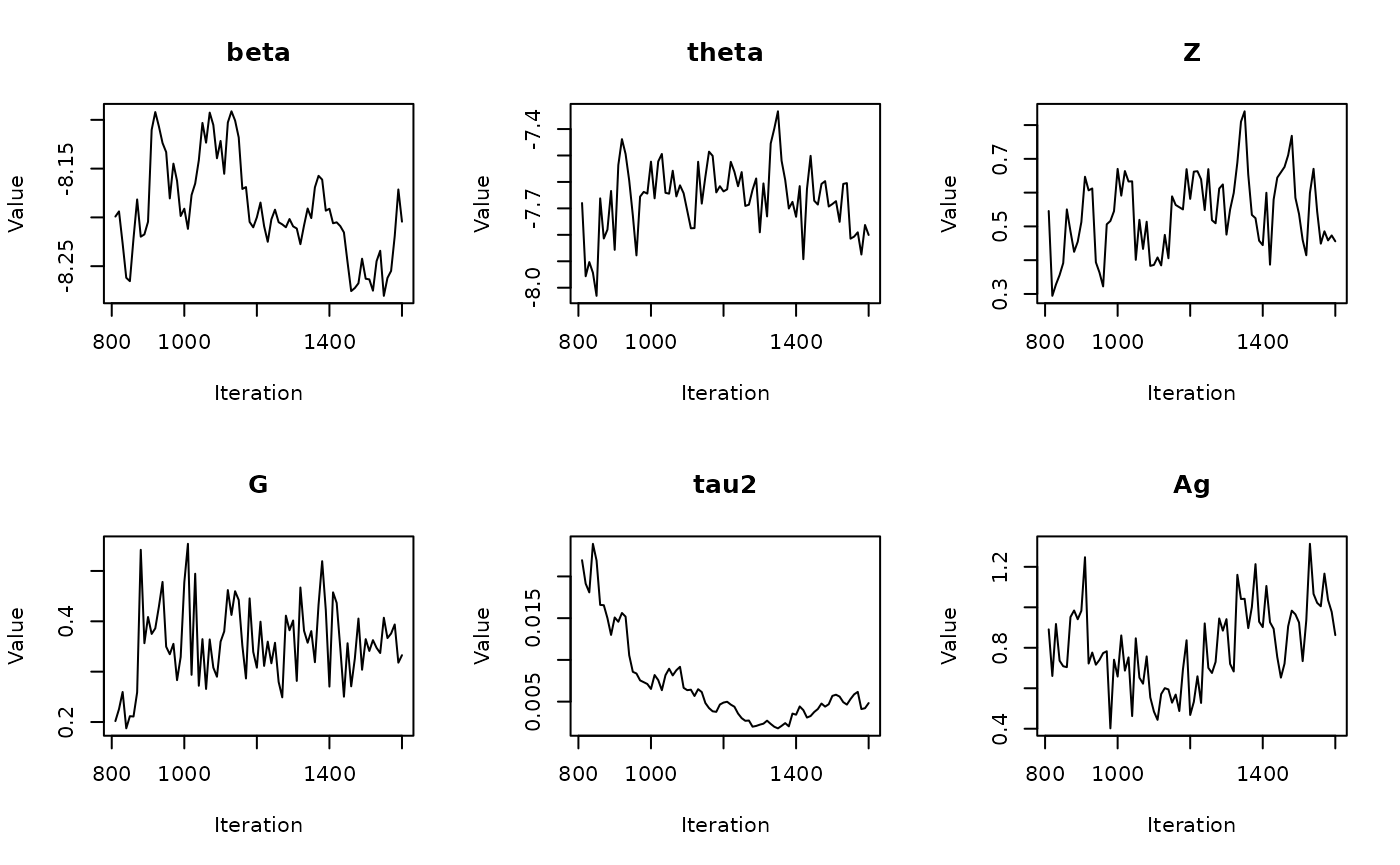
#> Batch 17/60, Progress: |..................................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |..................................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*.................................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*.................................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**................................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**................................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***...............................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***...............................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |****..............................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |****..............................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*****.............................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*****.............................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |******............................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |******............................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*******...........................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*******...........................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |********..........................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |********..........................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*********.........................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*********.........................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**********........................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**********........................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***********.......................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***********.......................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |************......................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |************......................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*************.....................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*************.....................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**************....................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**************....................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***************...................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***************...................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |****************..................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |****************..................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*****************.................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*****************.................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |******************................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |******************................................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*******************...............................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*******************...............................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |********************..............................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |********************..............................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*********************.............................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*********************.............................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**********************............................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**********************............................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***********************...........................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***********************...........................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |************************..........................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |************************..........................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*************************.........................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*************************.........................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**************************........................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**************************........................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***************************.......................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***************************.......................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |****************************......................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |****************************......................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*****************************.....................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*****************************.....................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |******************************....................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |******************************....................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*******************************...................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*******************************...................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |********************************..................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |********************************..................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*********************************.................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*********************************.................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**********************************................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**********************************................| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***********************************...............| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***********************************...............| Elapsed Time: 00:00:06 Batch 17/60, Progress: |************************************..............| Elapsed Time: 00:00:06 Batch 17/60, Progress: |************************************..............| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*************************************.............| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*************************************.............| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**************************************............| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**************************************............| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***************************************...........| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***************************************...........| Elapsed Time: 00:00:06 Batch 17/60, Progress: |****************************************..........| Elapsed Time: 00:00:06 Batch 17/60, Progress: |****************************************..........| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*****************************************.........| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*****************************************.........| Elapsed Time: 00:00:06 Batch 17/60, Progress: |******************************************........| Elapsed Time: 00:00:06 Batch 17/60, Progress: |******************************************........| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*******************************************.......| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*******************************************.......| Elapsed Time: 00:00:06 Batch 17/60, Progress: |********************************************......| Elapsed Time: 00:00:06 Batch 17/60, Progress: |********************************************......| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*********************************************.....| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*********************************************.....| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**********************************************....| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**********************************************....| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***********************************************...| Elapsed Time: 00:00:06 Batch 17/60, Progress: |***********************************************...| Elapsed Time: 00:00:06 Batch 17/60, Progress: |************************************************..| Elapsed Time: 00:00:06 Batch 17/60, Progress: |************************************************..| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*************************************************.| Elapsed Time: 00:00:06 Batch 17/60, Progress: |*************************************************.| Elapsed Time: 00:00:06 Batch 17/60, Progress: |**************************************************| Elapsed Time: 00:00:06 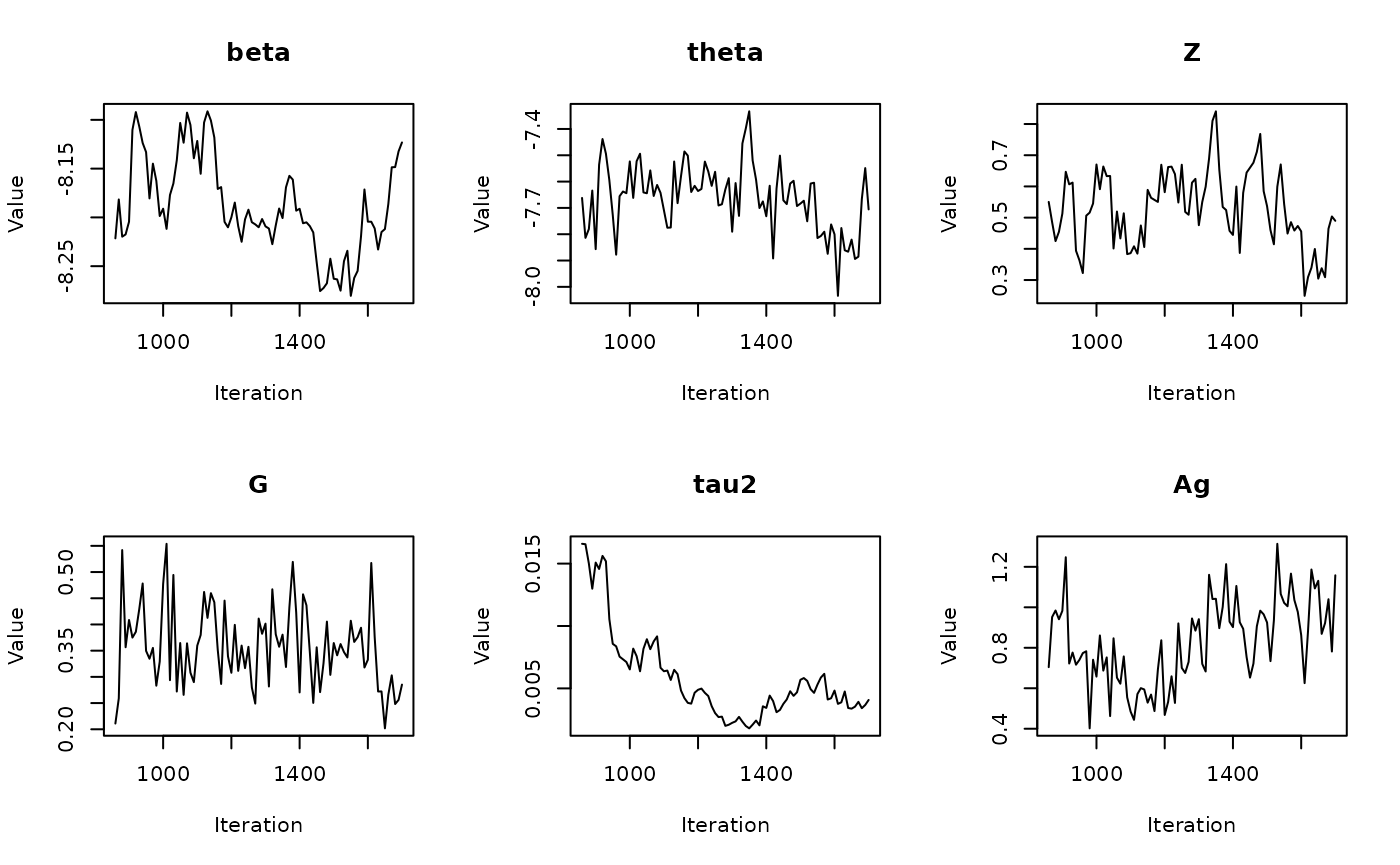
#> Batch 18/60, Progress: |..................................................| Elapsed Time: 00:00:06 Batch 18/60, Progress: |..................................................| Elapsed Time: 00:00:06 Batch 18/60, Progress: |*.................................................| Elapsed Time: 00:00:06 Batch 18/60, Progress: |*.................................................| Elapsed Time: 00:00:06 Batch 18/60, Progress: |**................................................| Elapsed Time: 00:00:06 Batch 18/60, Progress: |**................................................| Elapsed Time: 00:00:06 Batch 18/60, Progress: |***...............................................| Elapsed Time: 00:00:06 Batch 18/60, Progress: |***...............................................| Elapsed Time: 00:00:06 Batch 18/60, Progress: |****..............................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |****..............................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*****.............................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*****.............................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |******............................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |******............................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*******...........................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*******...........................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |********..........................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |********..........................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*********.........................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*********.........................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**********........................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**********........................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***********.......................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***********.......................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |************......................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |************......................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*************.....................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*************.....................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**************....................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**************....................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***************...................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***************...................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |****************..................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |****************..................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*****************.................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*****************.................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |******************................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |******************................................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*******************...............................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*******************...............................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |********************..............................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |********************..............................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*********************.............................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*********************.............................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**********************............................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**********************............................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***********************...........................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***********************...........................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |************************..........................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |************************..........................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*************************.........................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*************************.........................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**************************........................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**************************........................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***************************.......................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***************************.......................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |****************************......................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |****************************......................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*****************************.....................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*****************************.....................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |******************************....................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |******************************....................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*******************************...................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*******************************...................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |********************************..................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |********************************..................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*********************************.................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*********************************.................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**********************************................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**********************************................| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***********************************...............| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***********************************...............| Elapsed Time: 00:00:07 Batch 18/60, Progress: |************************************..............| Elapsed Time: 00:00:07 Batch 18/60, Progress: |************************************..............| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*************************************.............| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*************************************.............| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**************************************............| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**************************************............| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***************************************...........| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***************************************...........| Elapsed Time: 00:00:07 Batch 18/60, Progress: |****************************************..........| Elapsed Time: 00:00:07 Batch 18/60, Progress: |****************************************..........| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*****************************************.........| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*****************************************.........| Elapsed Time: 00:00:07 Batch 18/60, Progress: |******************************************........| Elapsed Time: 00:00:07 Batch 18/60, Progress: |******************************************........| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*******************************************.......| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*******************************************.......| Elapsed Time: 00:00:07 Batch 18/60, Progress: |********************************************......| Elapsed Time: 00:00:07 Batch 18/60, Progress: |********************************************......| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*********************************************.....| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*********************************************.....| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**********************************************....| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**********************************************....| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***********************************************...| Elapsed Time: 00:00:07 Batch 18/60, Progress: |***********************************************...| Elapsed Time: 00:00:07 Batch 18/60, Progress: |************************************************..| Elapsed Time: 00:00:07 Batch 18/60, Progress: |************************************************..| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*************************************************.| Elapsed Time: 00:00:07 Batch 18/60, Progress: |*************************************************.| Elapsed Time: 00:00:07 Batch 18/60, Progress: |**************************************************| Elapsed Time: 00:00:07 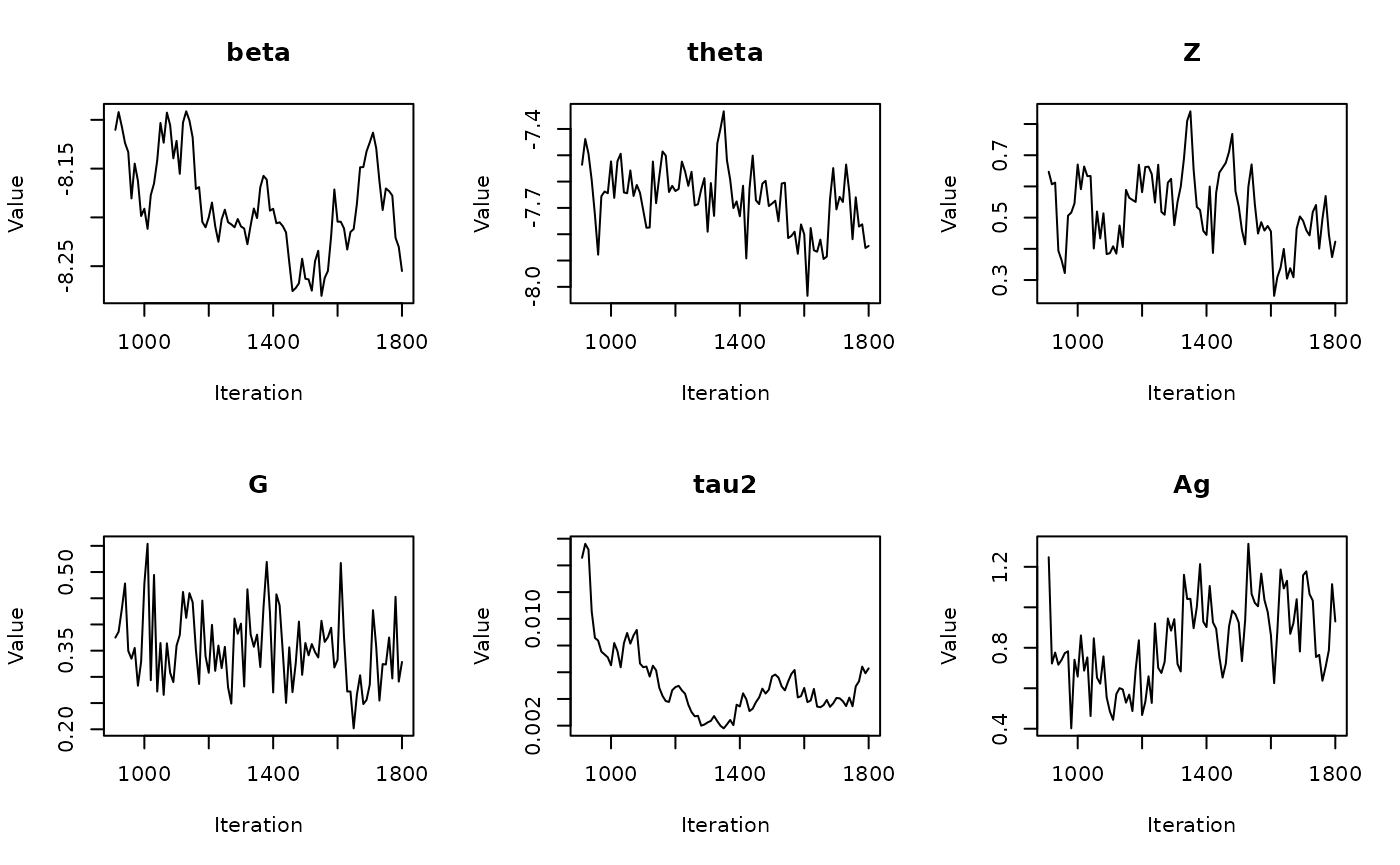
#> Batch 19/60, Progress: |..................................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |..................................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*.................................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*.................................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**................................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**................................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***...............................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***...............................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |****..............................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |****..............................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*****.............................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*****.............................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |******............................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |******............................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*******...........................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*******...........................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |********..........................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |********..........................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*********.........................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*********.........................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**********........................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**********........................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***********.......................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***********.......................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |************......................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |************......................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*************.....................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*************.....................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**************....................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**************....................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***************...................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***************...................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |****************..................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |****************..................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*****************.................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*****************.................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |******************................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |******************................................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*******************...............................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*******************...............................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |********************..............................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |********************..............................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*********************.............................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*********************.............................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**********************............................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**********************............................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***********************...........................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***********************...........................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |************************..........................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |************************..........................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*************************.........................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*************************.........................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**************************........................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**************************........................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***************************.......................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***************************.......................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |****************************......................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |****************************......................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*****************************.....................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*****************************.....................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |******************************....................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |******************************....................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*******************************...................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*******************************...................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |********************************..................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |********************************..................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*********************************.................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*********************************.................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**********************************................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**********************************................| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***********************************...............| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***********************************...............| Elapsed Time: 00:00:07 Batch 19/60, Progress: |************************************..............| Elapsed Time: 00:00:07 Batch 19/60, Progress: |************************************..............| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*************************************.............| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*************************************.............| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**************************************............| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**************************************............| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***************************************...........| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***************************************...........| Elapsed Time: 00:00:07 Batch 19/60, Progress: |****************************************..........| Elapsed Time: 00:00:07 Batch 19/60, Progress: |****************************************..........| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*****************************************.........| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*****************************************.........| Elapsed Time: 00:00:07 Batch 19/60, Progress: |******************************************........| Elapsed Time: 00:00:07 Batch 19/60, Progress: |******************************************........| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*******************************************.......| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*******************************************.......| Elapsed Time: 00:00:07 Batch 19/60, Progress: |********************************************......| Elapsed Time: 00:00:07 Batch 19/60, Progress: |********************************************......| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*********************************************.....| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*********************************************.....| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**********************************************....| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**********************************************....| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***********************************************...| Elapsed Time: 00:00:07 Batch 19/60, Progress: |***********************************************...| Elapsed Time: 00:00:07 Batch 19/60, Progress: |************************************************..| Elapsed Time: 00:00:07 Batch 19/60, Progress: |************************************************..| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*************************************************.| Elapsed Time: 00:00:07 Batch 19/60, Progress: |*************************************************.| Elapsed Time: 00:00:07 Batch 19/60, Progress: |**************************************************| Elapsed Time: 00:00:07 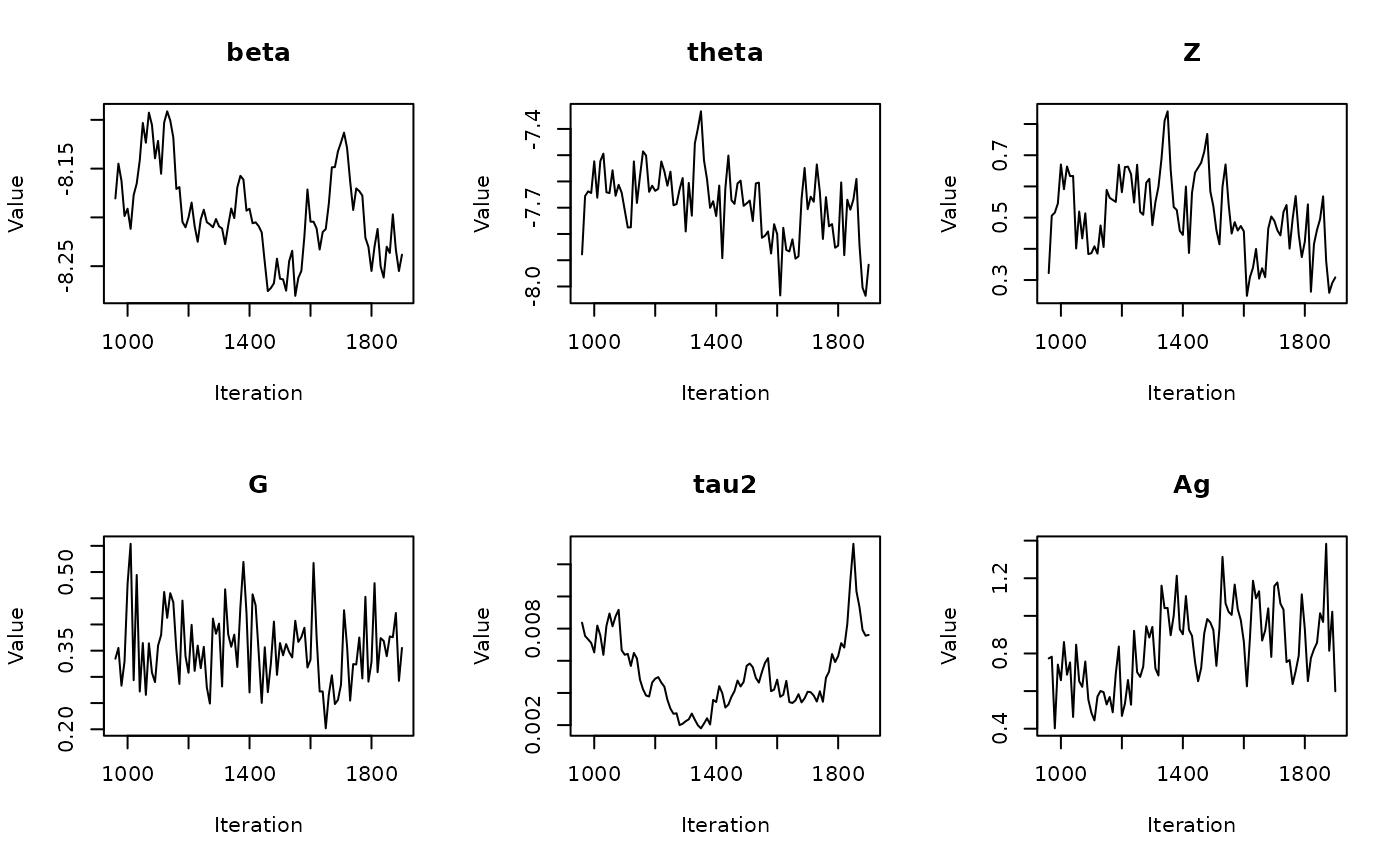
#> Batch 20/60, Progress: |..................................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |..................................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*.................................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*.................................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**................................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**................................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***...............................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***...............................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |****..............................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |****..............................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*****.............................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*****.............................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |******............................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |******............................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*******...........................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*******...........................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |********..........................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |********..........................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*********.........................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*********.........................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**********........................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**********........................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***********.......................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***********.......................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |************......................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |************......................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*************.....................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*************.....................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**************....................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**************....................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***************...................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***************...................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |****************..................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |****************..................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*****************.................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*****************.................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |******************................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |******************................................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*******************...............................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*******************...............................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |********************..............................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |********************..............................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*********************.............................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*********************.............................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**********************............................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**********************............................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***********************...........................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***********************...........................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |************************..........................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |************************..........................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*************************.........................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*************************.........................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**************************........................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**************************........................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***************************.......................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***************************.......................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |****************************......................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |****************************......................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*****************************.....................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*****************************.....................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |******************************....................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |******************************....................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*******************************...................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*******************************...................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |********************************..................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |********************************..................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*********************************.................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |*********************************.................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**********************************................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |**********************************................| Elapsed Time: 00:00:07 Batch 20/60, Progress: |***********************************...............| Elapsed Time: 00:00:08 Batch 20/60, Progress: |***********************************...............| Elapsed Time: 00:00:08 Batch 20/60, Progress: |************************************..............| Elapsed Time: 00:00:08 Batch 20/60, Progress: |************************************..............| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*************************************.............| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*************************************.............| Elapsed Time: 00:00:08 Batch 20/60, Progress: |**************************************............| Elapsed Time: 00:00:08 Batch 20/60, Progress: |**************************************............| Elapsed Time: 00:00:08 Batch 20/60, Progress: |***************************************...........| Elapsed Time: 00:00:08 Batch 20/60, Progress: |***************************************...........| Elapsed Time: 00:00:08 Batch 20/60, Progress: |****************************************..........| Elapsed Time: 00:00:08 Batch 20/60, Progress: |****************************************..........| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*****************************************.........| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*****************************************.........| Elapsed Time: 00:00:08 Batch 20/60, Progress: |******************************************........| Elapsed Time: 00:00:08 Batch 20/60, Progress: |******************************************........| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*******************************************.......| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*******************************************.......| Elapsed Time: 00:00:08 Batch 20/60, Progress: |********************************************......| Elapsed Time: 00:00:08 Batch 20/60, Progress: |********************************************......| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*********************************************.....| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*********************************************.....| Elapsed Time: 00:00:08 Batch 20/60, Progress: |**********************************************....| Elapsed Time: 00:00:08 Batch 20/60, Progress: |**********************************************....| Elapsed Time: 00:00:08 Batch 20/60, Progress: |***********************************************...| Elapsed Time: 00:00:08 Batch 20/60, Progress: |***********************************************...| Elapsed Time: 00:00:08 Batch 20/60, Progress: |************************************************..| Elapsed Time: 00:00:08 Batch 20/60, Progress: |************************************************..| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*************************************************.| Elapsed Time: 00:00:08 Batch 20/60, Progress: |*************************************************.| Elapsed Time: 00:00:08 Batch 20/60, Progress: |**************************************************| Elapsed Time: 00:00:08 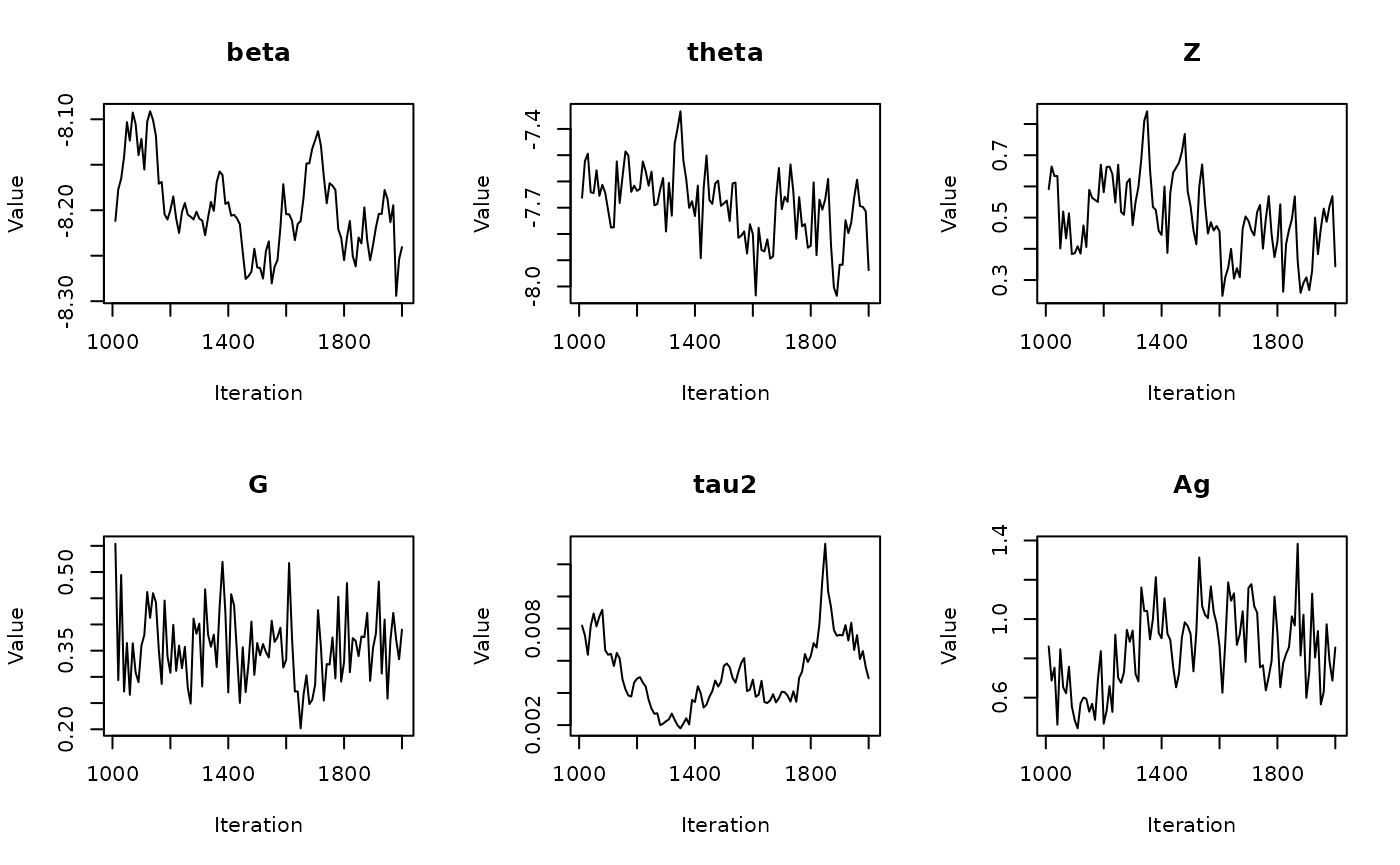
#> Batch 21/60, Progress: |..................................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |..................................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*.................................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*.................................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**................................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**................................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***...............................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***...............................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |****..............................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |****..............................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*****.............................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*****.............................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |******............................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |******............................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*******...........................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*******...........................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |********..........................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |********..........................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*********.........................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*********.........................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**********........................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**********........................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***********.......................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***********.......................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |************......................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |************......................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*************.....................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*************.....................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**************....................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**************....................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***************...................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***************...................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |****************..................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |****************..................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*****************.................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*****************.................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |******************................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |******************................................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*******************...............................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*******************...............................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |********************..............................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |********************..............................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*********************.............................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*********************.............................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**********************............................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**********************............................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***********************...........................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***********************...........................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |************************..........................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |************************..........................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*************************.........................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*************************.........................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**************************........................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**************************........................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***************************.......................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***************************.......................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |****************************......................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |****************************......................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*****************************.....................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*****************************.....................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |******************************....................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |******************************....................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*******************************...................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*******************************...................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |********************************..................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |********************************..................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*********************************.................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*********************************.................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**********************************................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**********************************................| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***********************************...............| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***********************************...............| Elapsed Time: 00:00:08 Batch 21/60, Progress: |************************************..............| Elapsed Time: 00:00:08 Batch 21/60, Progress: |************************************..............| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*************************************.............| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*************************************.............| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**************************************............| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**************************************............| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***************************************...........| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***************************************...........| Elapsed Time: 00:00:08 Batch 21/60, Progress: |****************************************..........| Elapsed Time: 00:00:08 Batch 21/60, Progress: |****************************************..........| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*****************************************.........| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*****************************************.........| Elapsed Time: 00:00:08 Batch 21/60, Progress: |******************************************........| Elapsed Time: 00:00:08 Batch 21/60, Progress: |******************************************........| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*******************************************.......| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*******************************************.......| Elapsed Time: 00:00:08 Batch 21/60, Progress: |********************************************......| Elapsed Time: 00:00:08 Batch 21/60, Progress: |********************************************......| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*********************************************.....| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*********************************************.....| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**********************************************....| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**********************************************....| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***********************************************...| Elapsed Time: 00:00:08 Batch 21/60, Progress: |***********************************************...| Elapsed Time: 00:00:08 Batch 21/60, Progress: |************************************************..| Elapsed Time: 00:00:08 Batch 21/60, Progress: |************************************************..| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*************************************************.| Elapsed Time: 00:00:08 Batch 21/60, Progress: |*************************************************.| Elapsed Time: 00:00:08 Batch 21/60, Progress: |**************************************************| Elapsed Time: 00:00:08 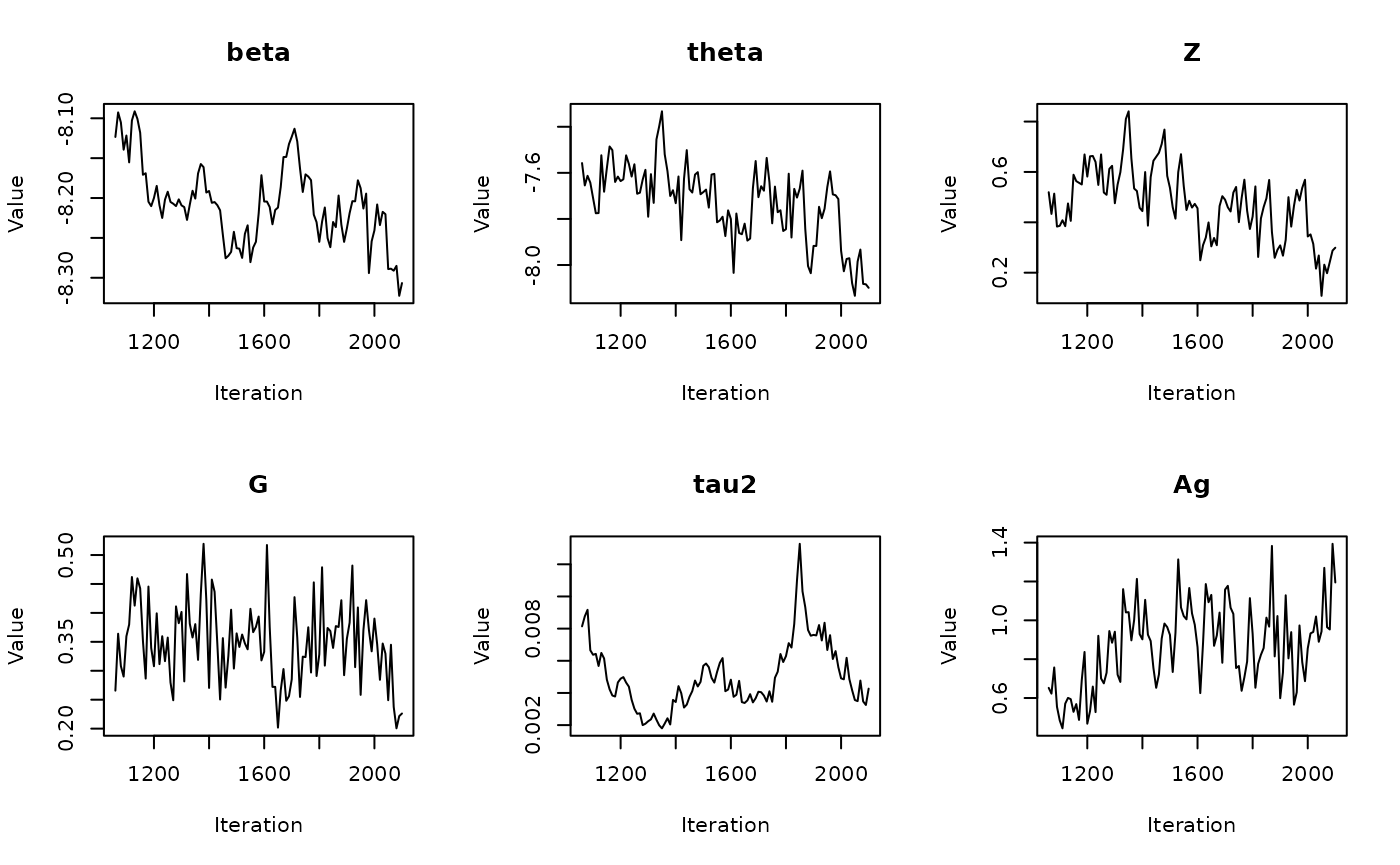
#> Batch 22/60, Progress: |..................................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |..................................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*.................................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*.................................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**................................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**................................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***...............................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***...............................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |****..............................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |****..............................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*****.............................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*****.............................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |******............................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |******............................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*******...........................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*******...........................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |********..........................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |********..........................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*********.........................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*********.........................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**********........................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**********........................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***********.......................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***********.......................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |************......................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |************......................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*************.....................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*************.....................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**************....................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**************....................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***************...................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***************...................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |****************..................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |****************..................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*****************.................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*****************.................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |******************................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |******************................................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*******************...............................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*******************...............................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |********************..............................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |********************..............................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*********************.............................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*********************.............................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**********************............................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**********************............................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***********************...........................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***********************...........................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |************************..........................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |************************..........................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*************************.........................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*************************.........................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**************************........................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**************************........................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***************************.......................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***************************.......................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |****************************......................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |****************************......................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*****************************.....................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*****************************.....................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |******************************....................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |******************************....................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*******************************...................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*******************************...................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |********************************..................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |********************************..................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*********************************.................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*********************************.................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**********************************................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**********************************................| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***********************************...............| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***********************************...............| Elapsed Time: 00:00:08 Batch 22/60, Progress: |************************************..............| Elapsed Time: 00:00:08 Batch 22/60, Progress: |************************************..............| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*************************************.............| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*************************************.............| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**************************************............| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**************************************............| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***************************************...........| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***************************************...........| Elapsed Time: 00:00:08 Batch 22/60, Progress: |****************************************..........| Elapsed Time: 00:00:08 Batch 22/60, Progress: |****************************************..........| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*****************************************.........| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*****************************************.........| Elapsed Time: 00:00:08 Batch 22/60, Progress: |******************************************........| Elapsed Time: 00:00:08 Batch 22/60, Progress: |******************************************........| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*******************************************.......| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*******************************************.......| Elapsed Time: 00:00:08 Batch 22/60, Progress: |********************************************......| Elapsed Time: 00:00:08 Batch 22/60, Progress: |********************************************......| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*********************************************.....| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*********************************************.....| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**********************************************....| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**********************************************....| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***********************************************...| Elapsed Time: 00:00:08 Batch 22/60, Progress: |***********************************************...| Elapsed Time: 00:00:08 Batch 22/60, Progress: |************************************************..| Elapsed Time: 00:00:08 Batch 22/60, Progress: |************************************************..| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*************************************************.| Elapsed Time: 00:00:08 Batch 22/60, Progress: |*************************************************.| Elapsed Time: 00:00:08 Batch 22/60, Progress: |**************************************************| Elapsed Time: 00:00:08 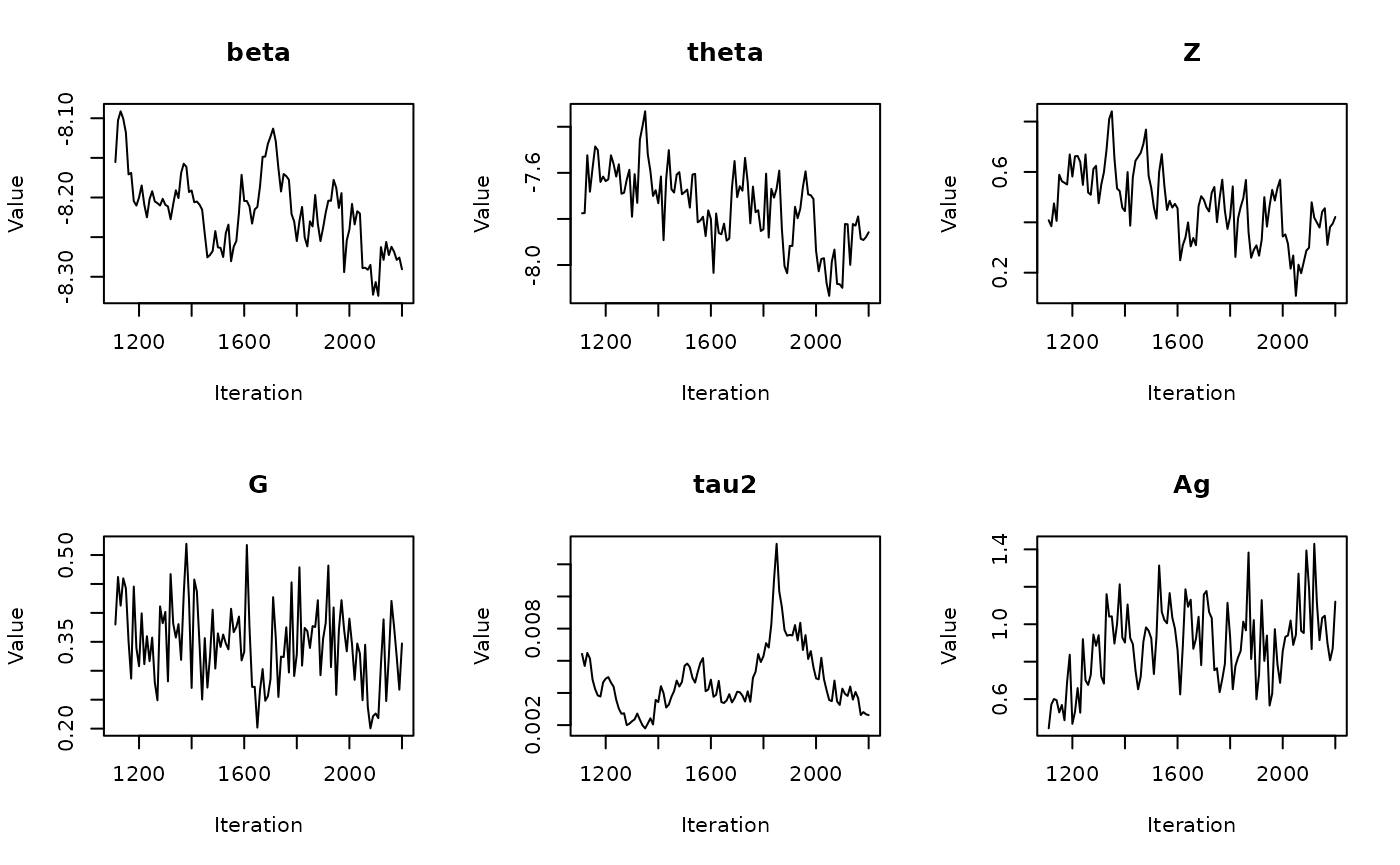
#> Batch 23/60, Progress: |..................................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |..................................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*.................................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*.................................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**................................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**................................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***...............................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***...............................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |****..............................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |****..............................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*****.............................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*****.............................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |******............................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |******............................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*******...........................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*******...........................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |********..........................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |********..........................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*********.........................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*********.........................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**********........................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**********........................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***********.......................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***********.......................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |************......................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |************......................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*************.....................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*************.....................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**************....................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**************....................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***************...................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***************...................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |****************..................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |****************..................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*****************.................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*****************.................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |******************................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |******************................................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*******************...............................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*******************...............................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |********************..............................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |********************..............................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*********************.............................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*********************.............................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**********************............................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**********************............................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***********************...........................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***********************...........................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |************************..........................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |************************..........................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*************************.........................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*************************.........................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**************************........................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**************************........................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***************************.......................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***************************.......................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |****************************......................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |****************************......................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*****************************.....................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*****************************.....................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |******************************....................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |******************************....................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*******************************...................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*******************************...................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |********************************..................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |********************************..................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*********************************.................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*********************************.................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**********************************................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**********************************................| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***********************************...............| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***********************************...............| Elapsed Time: 00:00:09 Batch 23/60, Progress: |************************************..............| Elapsed Time: 00:00:09 Batch 23/60, Progress: |************************************..............| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*************************************.............| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*************************************.............| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**************************************............| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**************************************............| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***************************************...........| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***************************************...........| Elapsed Time: 00:00:09 Batch 23/60, Progress: |****************************************..........| Elapsed Time: 00:00:09 Batch 23/60, Progress: |****************************************..........| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*****************************************.........| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*****************************************.........| Elapsed Time: 00:00:09 Batch 23/60, Progress: |******************************************........| Elapsed Time: 00:00:09 Batch 23/60, Progress: |******************************************........| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*******************************************.......| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*******************************************.......| Elapsed Time: 00:00:09 Batch 23/60, Progress: |********************************************......| Elapsed Time: 00:00:09 Batch 23/60, Progress: |********************************************......| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*********************************************.....| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*********************************************.....| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**********************************************....| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**********************************************....| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***********************************************...| Elapsed Time: 00:00:09 Batch 23/60, Progress: |***********************************************...| Elapsed Time: 00:00:09 Batch 23/60, Progress: |************************************************..| Elapsed Time: 00:00:09 Batch 23/60, Progress: |************************************************..| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*************************************************.| Elapsed Time: 00:00:09 Batch 23/60, Progress: |*************************************************.| Elapsed Time: 00:00:09 Batch 23/60, Progress: |**************************************************| Elapsed Time: 00:00:09 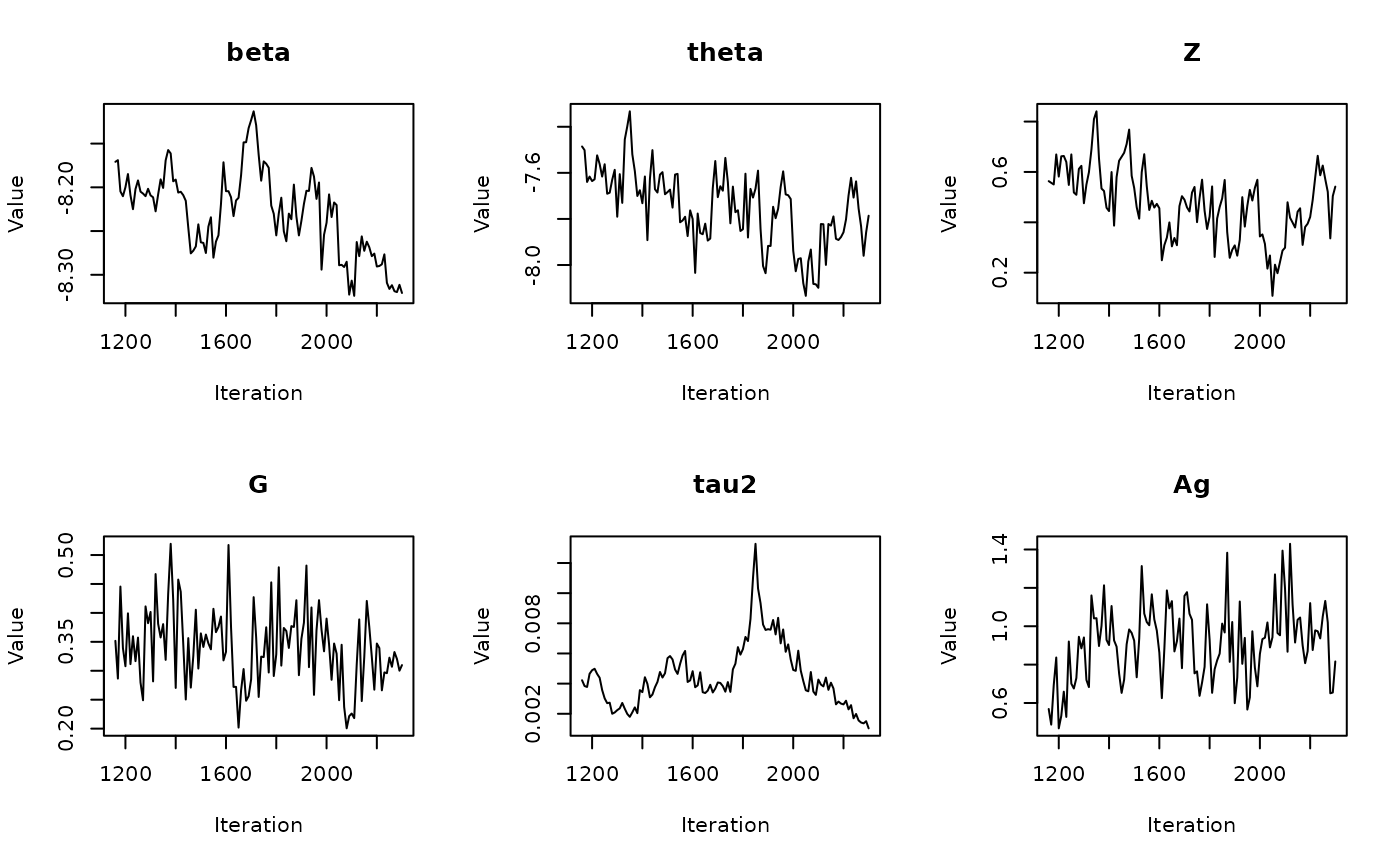
#> Batch 24/60, Progress: |..................................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |..................................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*.................................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*.................................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**................................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**................................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***...............................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***...............................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |****..............................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |****..............................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*****.............................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*****.............................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |******............................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |******............................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*******...........................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*******...........................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |********..........................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |********..........................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*********.........................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*********.........................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**********........................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**********........................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***********.......................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***********.......................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |************......................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |************......................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*************.....................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*************.....................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**************....................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**************....................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***************...................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***************...................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |****************..................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |****************..................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*****************.................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*****************.................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |******************................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |******************................................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*******************...............................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*******************...............................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |********************..............................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |********************..............................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*********************.............................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*********************.............................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**********************............................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**********************............................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***********************...........................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***********************...........................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |************************..........................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |************************..........................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*************************.........................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*************************.........................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**************************........................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**************************........................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***************************.......................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***************************.......................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |****************************......................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |****************************......................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*****************************.....................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*****************************.....................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |******************************....................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |******************************....................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*******************************...................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*******************************...................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |********************************..................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |********************************..................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*********************************.................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*********************************.................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**********************************................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**********************************................| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***********************************...............| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***********************************...............| Elapsed Time: 00:00:09 Batch 24/60, Progress: |************************************..............| Elapsed Time: 00:00:09 Batch 24/60, Progress: |************************************..............| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*************************************.............| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*************************************.............| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**************************************............| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**************************************............| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***************************************...........| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***************************************...........| Elapsed Time: 00:00:09 Batch 24/60, Progress: |****************************************..........| Elapsed Time: 00:00:09 Batch 24/60, Progress: |****************************************..........| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*****************************************.........| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*****************************************.........| Elapsed Time: 00:00:09 Batch 24/60, Progress: |******************************************........| Elapsed Time: 00:00:09 Batch 24/60, Progress: |******************************************........| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*******************************************.......| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*******************************************.......| Elapsed Time: 00:00:09 Batch 24/60, Progress: |********************************************......| Elapsed Time: 00:00:09 Batch 24/60, Progress: |********************************************......| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*********************************************.....| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*********************************************.....| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**********************************************....| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**********************************************....| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***********************************************...| Elapsed Time: 00:00:09 Batch 24/60, Progress: |***********************************************...| Elapsed Time: 00:00:09 Batch 24/60, Progress: |************************************************..| Elapsed Time: 00:00:09 Batch 24/60, Progress: |************************************************..| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*************************************************.| Elapsed Time: 00:00:09 Batch 24/60, Progress: |*************************************************.| Elapsed Time: 00:00:09 Batch 24/60, Progress: |**************************************************| Elapsed Time: 00:00:09 
#> Batch 25/60, Progress: |..................................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |..................................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*.................................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*.................................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**................................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**................................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |***...............................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |***...............................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |****..............................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |****..............................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*****.............................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*****.............................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |******............................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |******............................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*******...........................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*******...........................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |********..........................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |********..........................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*********.........................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*********.........................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**********........................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**********........................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |***********.......................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |***********.......................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |************......................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |************......................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*************.....................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*************.....................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**************....................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**************....................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |***************...................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |***************...................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |****************..................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |****************..................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*****************.................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*****************.................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |******************................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |******************................................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*******************...............................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*******************...............................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |********************..............................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |********************..............................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*********************.............................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*********************.............................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**********************............................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**********************............................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |***********************...........................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |***********************...........................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |************************..........................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |************************..........................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*************************.........................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |*************************.........................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**************************........................| Elapsed Time: 00:00:09 Batch 25/60, Progress: |**************************........................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |***************************.......................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |***************************.......................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |****************************......................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |****************************......................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*****************************.....................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*****************************.....................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |******************************....................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |******************************....................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*******************************...................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*******************************...................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |********************************..................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |********************************..................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*********************************.................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*********************************.................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |**********************************................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |**********************************................| Elapsed Time: 00:00:10 Batch 25/60, Progress: |***********************************...............| Elapsed Time: 00:00:10 Batch 25/60, Progress: |***********************************...............| Elapsed Time: 00:00:10 Batch 25/60, Progress: |************************************..............| Elapsed Time: 00:00:10 Batch 25/60, Progress: |************************************..............| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*************************************.............| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*************************************.............| Elapsed Time: 00:00:10 Batch 25/60, Progress: |**************************************............| Elapsed Time: 00:00:10 Batch 25/60, Progress: |**************************************............| Elapsed Time: 00:00:10 Batch 25/60, Progress: |***************************************...........| Elapsed Time: 00:00:10 Batch 25/60, Progress: |***************************************...........| Elapsed Time: 00:00:10 Batch 25/60, Progress: |****************************************..........| Elapsed Time: 00:00:10 Batch 25/60, Progress: |****************************************..........| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*****************************************.........| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*****************************************.........| Elapsed Time: 00:00:10 Batch 25/60, Progress: |******************************************........| Elapsed Time: 00:00:10 Batch 25/60, Progress: |******************************************........| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*******************************************.......| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*******************************************.......| Elapsed Time: 00:00:10 Batch 25/60, Progress: |********************************************......| Elapsed Time: 00:00:10 Batch 25/60, Progress: |********************************************......| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*********************************************.....| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*********************************************.....| Elapsed Time: 00:00:10 Batch 25/60, Progress: |**********************************************....| Elapsed Time: 00:00:10 Batch 25/60, Progress: |**********************************************....| Elapsed Time: 00:00:10 Batch 25/60, Progress: |***********************************************...| Elapsed Time: 00:00:10 Batch 25/60, Progress: |***********************************************...| Elapsed Time: 00:00:10 Batch 25/60, Progress: |************************************************..| Elapsed Time: 00:00:10 Batch 25/60, Progress: |************************************************..| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*************************************************.| Elapsed Time: 00:00:10 Batch 25/60, Progress: |*************************************************.| Elapsed Time: 00:00:10 Batch 25/60, Progress: |**************************************************| Elapsed Time: 00:00:10 
#> Batch 26/60, Progress: |..................................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |..................................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*.................................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*.................................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**................................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**................................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***...............................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***...............................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |****..............................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |****..............................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*****.............................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*****.............................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |******............................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |******............................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*******...........................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*******...........................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |********..........................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |********..........................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*********.........................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*********.........................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**********........................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**********........................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***********.......................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***********.......................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |************......................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |************......................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*************.....................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*************.....................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**************....................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**************....................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***************...................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***************...................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |****************..................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |****************..................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*****************.................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*****************.................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |******************................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |******************................................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*******************...............................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*******************...............................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |********************..............................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |********************..............................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*********************.............................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*********************.............................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**********************............................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**********************............................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***********************...........................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***********************...........................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |************************..........................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |************************..........................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*************************.........................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*************************.........................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**************************........................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**************************........................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***************************.......................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***************************.......................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |****************************......................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |****************************......................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*****************************.....................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*****************************.....................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |******************************....................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |******************************....................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*******************************...................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*******************************...................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |********************************..................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |********************************..................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*********************************.................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*********************************.................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**********************************................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**********************************................| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***********************************...............| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***********************************...............| Elapsed Time: 00:00:10 Batch 26/60, Progress: |************************************..............| Elapsed Time: 00:00:10 Batch 26/60, Progress: |************************************..............| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*************************************.............| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*************************************.............| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**************************************............| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**************************************............| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***************************************...........| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***************************************...........| Elapsed Time: 00:00:10 Batch 26/60, Progress: |****************************************..........| Elapsed Time: 00:00:10 Batch 26/60, Progress: |****************************************..........| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*****************************************.........| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*****************************************.........| Elapsed Time: 00:00:10 Batch 26/60, Progress: |******************************************........| Elapsed Time: 00:00:10 Batch 26/60, Progress: |******************************************........| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*******************************************.......| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*******************************************.......| Elapsed Time: 00:00:10 Batch 26/60, Progress: |********************************************......| Elapsed Time: 00:00:10 Batch 26/60, Progress: |********************************************......| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*********************************************.....| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*********************************************.....| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**********************************************....| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**********************************************....| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***********************************************...| Elapsed Time: 00:00:10 Batch 26/60, Progress: |***********************************************...| Elapsed Time: 00:00:10 Batch 26/60, Progress: |************************************************..| Elapsed Time: 00:00:10 Batch 26/60, Progress: |************************************************..| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*************************************************.| Elapsed Time: 00:00:10 Batch 26/60, Progress: |*************************************************.| Elapsed Time: 00:00:10 Batch 26/60, Progress: |**************************************************| Elapsed Time: 00:00:10 
#> Batch 27/60, Progress: |..................................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |..................................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*.................................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*.................................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**................................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**................................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***...............................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***...............................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |****..............................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |****..............................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*****.............................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*****.............................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |******............................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |******............................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*******...........................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*******...........................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |********..........................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |********..........................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*********.........................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*********.........................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**********........................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**********........................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***********.......................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***********.......................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |************......................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |************......................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*************.....................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*************.....................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**************....................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**************....................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***************...................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***************...................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |****************..................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |****************..................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*****************.................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*****************.................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |******************................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |******************................................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*******************...............................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*******************...............................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |********************..............................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |********************..............................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*********************.............................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*********************.............................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**********************............................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**********************............................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***********************...........................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***********************...........................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |************************..........................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |************************..........................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*************************.........................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*************************.........................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**************************........................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**************************........................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***************************.......................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***************************.......................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |****************************......................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |****************************......................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*****************************.....................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*****************************.....................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |******************************....................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |******************************....................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*******************************...................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*******************************...................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |********************************..................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |********************************..................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*********************************.................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*********************************.................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**********************************................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**********************************................| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***********************************...............| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***********************************...............| Elapsed Time: 00:00:10 Batch 27/60, Progress: |************************************..............| Elapsed Time: 00:00:10 Batch 27/60, Progress: |************************************..............| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*************************************.............| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*************************************.............| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**************************************............| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**************************************............| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***************************************...........| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***************************************...........| Elapsed Time: 00:00:10 Batch 27/60, Progress: |****************************************..........| Elapsed Time: 00:00:10 Batch 27/60, Progress: |****************************************..........| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*****************************************.........| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*****************************************.........| Elapsed Time: 00:00:10 Batch 27/60, Progress: |******************************************........| Elapsed Time: 00:00:10 Batch 27/60, Progress: |******************************************........| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*******************************************.......| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*******************************************.......| Elapsed Time: 00:00:10 Batch 27/60, Progress: |********************************************......| Elapsed Time: 00:00:10 Batch 27/60, Progress: |********************************************......| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*********************************************.....| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*********************************************.....| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**********************************************....| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**********************************************....| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***********************************************...| Elapsed Time: 00:00:10 Batch 27/60, Progress: |***********************************************...| Elapsed Time: 00:00:10 Batch 27/60, Progress: |************************************************..| Elapsed Time: 00:00:10 Batch 27/60, Progress: |************************************************..| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*************************************************.| Elapsed Time: 00:00:10 Batch 27/60, Progress: |*************************************************.| Elapsed Time: 00:00:10 Batch 27/60, Progress: |**************************************************| Elapsed Time: 00:00:10 
#> Batch 28/60, Progress: |..................................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |..................................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*.................................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*.................................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**................................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**................................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***...............................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***...............................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |****..............................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |****..............................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*****.............................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*****.............................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |******............................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |******............................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*******...........................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*******...........................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |********..........................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |********..........................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*********.........................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*********.........................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**********........................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**********........................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***********.......................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***********.......................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |************......................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |************......................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*************.....................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*************.....................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**************....................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**************....................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***************...................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***************...................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |****************..................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |****************..................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*****************.................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*****************.................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |******************................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |******************................................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*******************...............................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*******************...............................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |********************..............................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |********************..............................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*********************.............................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*********************.............................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**********************............................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**********************............................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***********************...........................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***********************...........................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |************************..........................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |************************..........................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*************************.........................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*************************.........................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**************************........................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**************************........................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***************************.......................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***************************.......................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |****************************......................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |****************************......................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*****************************.....................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*****************************.....................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |******************************....................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |******************************....................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*******************************...................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*******************************...................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |********************************..................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |********************************..................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*********************************.................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*********************************.................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**********************************................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**********************************................| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***********************************...............| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***********************************...............| Elapsed Time: 00:00:11 Batch 28/60, Progress: |************************************..............| Elapsed Time: 00:00:11 Batch 28/60, Progress: |************************************..............| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*************************************.............| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*************************************.............| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**************************************............| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**************************************............| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***************************************...........| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***************************************...........| Elapsed Time: 00:00:11 Batch 28/60, Progress: |****************************************..........| Elapsed Time: 00:00:11 Batch 28/60, Progress: |****************************************..........| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*****************************************.........| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*****************************************.........| Elapsed Time: 00:00:11 Batch 28/60, Progress: |******************************************........| Elapsed Time: 00:00:11 Batch 28/60, Progress: |******************************************........| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*******************************************.......| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*******************************************.......| Elapsed Time: 00:00:11 Batch 28/60, Progress: |********************************************......| Elapsed Time: 00:00:11 Batch 28/60, Progress: |********************************************......| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*********************************************.....| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*********************************************.....| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**********************************************....| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**********************************************....| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***********************************************...| Elapsed Time: 00:00:11 Batch 28/60, Progress: |***********************************************...| Elapsed Time: 00:00:11 Batch 28/60, Progress: |************************************************..| Elapsed Time: 00:00:11 Batch 28/60, Progress: |************************************************..| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*************************************************.| Elapsed Time: 00:00:11 Batch 28/60, Progress: |*************************************************.| Elapsed Time: 00:00:11 Batch 28/60, Progress: |**************************************************| Elapsed Time: 00:00:11 
#> Batch 29/60, Progress: |..................................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |..................................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*.................................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*.................................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**................................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**................................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***...............................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***...............................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |****..............................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |****..............................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*****.............................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*****.............................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |******............................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |******............................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*******...........................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*******...........................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |********..........................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |********..........................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*********.........................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*********.........................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**********........................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**********........................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***********.......................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***********.......................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |************......................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |************......................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*************.....................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*************.....................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**************....................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**************....................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***************...................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***************...................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |****************..................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |****************..................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*****************.................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*****************.................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |******************................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |******************................................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*******************...............................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*******************...............................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |********************..............................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |********************..............................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*********************.............................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*********************.............................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**********************............................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**********************............................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***********************...........................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***********************...........................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |************************..........................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |************************..........................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*************************.........................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*************************.........................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**************************........................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**************************........................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***************************.......................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***************************.......................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |****************************......................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |****************************......................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*****************************.....................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*****************************.....................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |******************************....................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |******************************....................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*******************************...................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*******************************...................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |********************************..................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |********************************..................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*********************************.................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*********************************.................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**********************************................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**********************************................| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***********************************...............| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***********************************...............| Elapsed Time: 00:00:11 Batch 29/60, Progress: |************************************..............| Elapsed Time: 00:00:11 Batch 29/60, Progress: |************************************..............| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*************************************.............| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*************************************.............| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**************************************............| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**************************************............| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***************************************...........| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***************************************...........| Elapsed Time: 00:00:11 Batch 29/60, Progress: |****************************************..........| Elapsed Time: 00:00:11 Batch 29/60, Progress: |****************************************..........| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*****************************************.........| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*****************************************.........| Elapsed Time: 00:00:11 Batch 29/60, Progress: |******************************************........| Elapsed Time: 00:00:11 Batch 29/60, Progress: |******************************************........| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*******************************************.......| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*******************************************.......| Elapsed Time: 00:00:11 Batch 29/60, Progress: |********************************************......| Elapsed Time: 00:00:11 Batch 29/60, Progress: |********************************************......| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*********************************************.....| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*********************************************.....| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**********************************************....| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**********************************************....| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***********************************************...| Elapsed Time: 00:00:11 Batch 29/60, Progress: |***********************************************...| Elapsed Time: 00:00:11 Batch 29/60, Progress: |************************************************..| Elapsed Time: 00:00:11 Batch 29/60, Progress: |************************************************..| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*************************************************.| Elapsed Time: 00:00:11 Batch 29/60, Progress: |*************************************************.| Elapsed Time: 00:00:11 Batch 29/60, Progress: |**************************************************| Elapsed Time: 00:00:11 
#> Batch 30/60, Progress: |..................................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |..................................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |*.................................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |*.................................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |**................................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |**................................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |***...............................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |***...............................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |****..............................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |****..............................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |*****.............................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |*****.............................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |******............................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |******............................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |*******...........................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |*******...........................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |********..........................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |********..........................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |*********.........................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |*********.........................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |**********........................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |**********........................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |***********.......................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |***********.......................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |************......................................| Elapsed Time: 00:00:11 Batch 30/60, Progress: |************......................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*************.....................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*************.....................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**************....................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**************....................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***************...................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***************...................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |****************..................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |****************..................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*****************.................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*****************.................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |******************................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |******************................................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*******************...............................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*******************...............................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |********************..............................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |********************..............................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*********************.............................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*********************.............................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**********************............................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**********************............................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***********************...........................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***********************...........................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |************************..........................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |************************..........................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*************************.........................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*************************.........................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**************************........................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**************************........................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***************************.......................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***************************.......................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |****************************......................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |****************************......................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*****************************.....................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*****************************.....................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |******************************....................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |******************************....................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*******************************...................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*******************************...................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |********************************..................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |********************************..................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*********************************.................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*********************************.................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**********************************................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**********************************................| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***********************************...............| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***********************************...............| Elapsed Time: 00:00:12 Batch 30/60, Progress: |************************************..............| Elapsed Time: 00:00:12 Batch 30/60, Progress: |************************************..............| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*************************************.............| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*************************************.............| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**************************************............| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**************************************............| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***************************************...........| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***************************************...........| Elapsed Time: 00:00:12 Batch 30/60, Progress: |****************************************..........| Elapsed Time: 00:00:12 Batch 30/60, Progress: |****************************************..........| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*****************************************.........| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*****************************************.........| Elapsed Time: 00:00:12 Batch 30/60, Progress: |******************************************........| Elapsed Time: 00:00:12 Batch 30/60, Progress: |******************************************........| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*******************************************.......| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*******************************************.......| Elapsed Time: 00:00:12 Batch 30/60, Progress: |********************************************......| Elapsed Time: 00:00:12 Batch 30/60, Progress: |********************************************......| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*********************************************.....| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*********************************************.....| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**********************************************....| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**********************************************....| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***********************************************...| Elapsed Time: 00:00:12 Batch 30/60, Progress: |***********************************************...| Elapsed Time: 00:00:12 Batch 30/60, Progress: |************************************************..| Elapsed Time: 00:00:12 Batch 30/60, Progress: |************************************************..| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*************************************************.| Elapsed Time: 00:00:12 Batch 30/60, Progress: |*************************************************.| Elapsed Time: 00:00:12 Batch 30/60, Progress: |**************************************************| Elapsed Time: 00:00:12 
#> Batch 31/60, Progress: |..................................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |..................................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*.................................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*.................................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**................................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**................................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***...............................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***...............................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |****..............................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |****..............................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*****.............................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*****.............................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |******............................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |******............................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*******...........................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*******...........................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |********..........................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |********..........................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*********.........................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*********.........................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**********........................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**********........................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***********.......................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***********.......................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |************......................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |************......................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*************.....................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*************.....................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**************....................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**************....................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***************...................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***************...................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |****************..................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |****************..................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*****************.................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*****************.................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |******************................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |******************................................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*******************...............................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*******************...............................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |********************..............................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |********************..............................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*********************.............................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*********************.............................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**********************............................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**********************............................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***********************...........................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***********************...........................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |************************..........................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |************************..........................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*************************.........................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*************************.........................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**************************........................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**************************........................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***************************.......................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***************************.......................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |****************************......................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |****************************......................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*****************************.....................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*****************************.....................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |******************************....................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |******************************....................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*******************************...................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*******************************...................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |********************************..................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |********************************..................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*********************************.................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*********************************.................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**********************************................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**********************************................| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***********************************...............| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***********************************...............| Elapsed Time: 00:00:12 Batch 31/60, Progress: |************************************..............| Elapsed Time: 00:00:12 Batch 31/60, Progress: |************************************..............| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*************************************.............| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*************************************.............| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**************************************............| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**************************************............| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***************************************...........| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***************************************...........| Elapsed Time: 00:00:12 Batch 31/60, Progress: |****************************************..........| Elapsed Time: 00:00:12 Batch 31/60, Progress: |****************************************..........| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*****************************************.........| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*****************************************.........| Elapsed Time: 00:00:12 Batch 31/60, Progress: |******************************************........| Elapsed Time: 00:00:12 Batch 31/60, Progress: |******************************************........| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*******************************************.......| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*******************************************.......| Elapsed Time: 00:00:12 Batch 31/60, Progress: |********************************************......| Elapsed Time: 00:00:12 Batch 31/60, Progress: |********************************************......| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*********************************************.....| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*********************************************.....| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**********************************************....| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**********************************************....| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***********************************************...| Elapsed Time: 00:00:12 Batch 31/60, Progress: |***********************************************...| Elapsed Time: 00:00:12 Batch 31/60, Progress: |************************************************..| Elapsed Time: 00:00:12 Batch 31/60, Progress: |************************************************..| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*************************************************.| Elapsed Time: 00:00:12 Batch 31/60, Progress: |*************************************************.| Elapsed Time: 00:00:12 Batch 31/60, Progress: |**************************************************| Elapsed Time: 00:00:12 
#> Batch 32/60, Progress: |..................................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |..................................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*.................................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*.................................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**................................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**................................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***...............................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***...............................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |****..............................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |****..............................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*****.............................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*****.............................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |******............................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |******............................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*******...........................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*******...........................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |********..........................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |********..........................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*********.........................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*********.........................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**********........................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**********........................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***********.......................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***********.......................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |************......................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |************......................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*************.....................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*************.....................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**************....................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**************....................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***************...................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***************...................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |****************..................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |****************..................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*****************.................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*****************.................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |******************................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |******************................................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*******************...............................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*******************...............................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |********************..............................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |********************..............................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*********************.............................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*********************.............................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**********************............................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**********************............................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***********************...........................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***********************...........................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |************************..........................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |************************..........................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*************************.........................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*************************.........................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**************************........................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**************************........................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***************************.......................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***************************.......................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |****************************......................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |****************************......................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*****************************.....................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*****************************.....................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |******************************....................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |******************************....................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*******************************...................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*******************************...................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |********************************..................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |********************************..................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*********************************.................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*********************************.................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**********************************................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**********************************................| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***********************************...............| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***********************************...............| Elapsed Time: 00:00:12 Batch 32/60, Progress: |************************************..............| Elapsed Time: 00:00:12 Batch 32/60, Progress: |************************************..............| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*************************************.............| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*************************************.............| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**************************************............| Elapsed Time: 00:00:12 Batch 32/60, Progress: |**************************************............| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***************************************...........| Elapsed Time: 00:00:12 Batch 32/60, Progress: |***************************************...........| Elapsed Time: 00:00:12 Batch 32/60, Progress: |****************************************..........| Elapsed Time: 00:00:12 Batch 32/60, Progress: |****************************************..........| Elapsed Time: 00:00:12 Batch 32/60, Progress: |*****************************************.........| Elapsed Time: 00:00:13 Batch 32/60, Progress: |*****************************************.........| Elapsed Time: 00:00:13 Batch 32/60, Progress: |******************************************........| Elapsed Time: 00:00:13 Batch 32/60, Progress: |******************************************........| Elapsed Time: 00:00:13 Batch 32/60, Progress: |*******************************************.......| Elapsed Time: 00:00:13 Batch 32/60, Progress: |*******************************************.......| Elapsed Time: 00:00:13 Batch 32/60, Progress: |********************************************......| Elapsed Time: 00:00:13 Batch 32/60, Progress: |********************************************......| Elapsed Time: 00:00:13 Batch 32/60, Progress: |*********************************************.....| Elapsed Time: 00:00:13 Batch 32/60, Progress: |*********************************************.....| Elapsed Time: 00:00:13 Batch 32/60, Progress: |**********************************************....| Elapsed Time: 00:00:13 Batch 32/60, Progress: |**********************************************....| Elapsed Time: 00:00:13 Batch 32/60, Progress: |***********************************************...| Elapsed Time: 00:00:13 Batch 32/60, Progress: |***********************************************...| Elapsed Time: 00:00:13 Batch 32/60, Progress: |************************************************..| Elapsed Time: 00:00:13 Batch 32/60, Progress: |************************************************..| Elapsed Time: 00:00:13 Batch 32/60, Progress: |*************************************************.| Elapsed Time: 00:00:13 Batch 32/60, Progress: |*************************************************.| Elapsed Time: 00:00:13 Batch 32/60, Progress: |**************************************************| Elapsed Time: 00:00:13 
#> Batch 33/60, Progress: |..................................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |..................................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*.................................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*.................................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**................................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**................................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***...............................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***...............................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |****..............................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |****..............................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*****.............................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*****.............................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |******............................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |******............................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*******...........................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*******...........................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |********..........................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |********..........................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*********.........................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*********.........................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**********........................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**********........................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***********.......................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***********.......................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |************......................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |************......................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*************.....................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*************.....................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**************....................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**************....................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***************...................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***************...................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |****************..................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |****************..................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*****************.................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*****************.................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |******************................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |******************................................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*******************...............................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*******************...............................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |********************..............................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |********************..............................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*********************.............................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*********************.............................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**********************............................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**********************............................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***********************...........................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***********************...........................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |************************..........................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |************************..........................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*************************.........................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*************************.........................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**************************........................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**************************........................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***************************.......................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***************************.......................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |****************************......................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |****************************......................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*****************************.....................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*****************************.....................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |******************************....................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |******************************....................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*******************************...................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*******************************...................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |********************************..................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |********************************..................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*********************************.................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*********************************.................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**********************************................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**********************************................| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***********************************...............| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***********************************...............| Elapsed Time: 00:00:13 Batch 33/60, Progress: |************************************..............| Elapsed Time: 00:00:13 Batch 33/60, Progress: |************************************..............| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*************************************.............| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*************************************.............| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**************************************............| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**************************************............| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***************************************...........| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***************************************...........| Elapsed Time: 00:00:13 Batch 33/60, Progress: |****************************************..........| Elapsed Time: 00:00:13 Batch 33/60, Progress: |****************************************..........| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*****************************************.........| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*****************************************.........| Elapsed Time: 00:00:13 Batch 33/60, Progress: |******************************************........| Elapsed Time: 00:00:13 Batch 33/60, Progress: |******************************************........| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*******************************************.......| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*******************************************.......| Elapsed Time: 00:00:13 Batch 33/60, Progress: |********************************************......| Elapsed Time: 00:00:13 Batch 33/60, Progress: |********************************************......| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*********************************************.....| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*********************************************.....| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**********************************************....| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**********************************************....| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***********************************************...| Elapsed Time: 00:00:13 Batch 33/60, Progress: |***********************************************...| Elapsed Time: 00:00:13 Batch 33/60, Progress: |************************************************..| Elapsed Time: 00:00:13 Batch 33/60, Progress: |************************************************..| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*************************************************.| Elapsed Time: 00:00:13 Batch 33/60, Progress: |*************************************************.| Elapsed Time: 00:00:13 Batch 33/60, Progress: |**************************************************| Elapsed Time: 00:00:13 
#> Batch 34/60, Progress: |..................................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |..................................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*.................................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*.................................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**................................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**................................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***...............................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***...............................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |****..............................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |****..............................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*****.............................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*****.............................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |******............................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |******............................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*******...........................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*******...........................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |********..........................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |********..........................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*********.........................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*********.........................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**********........................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**********........................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***********.......................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***********.......................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |************......................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |************......................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*************.....................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*************.....................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**************....................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**************....................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***************...................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***************...................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |****************..................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |****************..................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*****************.................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*****************.................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |******************................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |******************................................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*******************...............................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*******************...............................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |********************..............................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |********************..............................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*********************.............................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*********************.............................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**********************............................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**********************............................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***********************...........................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***********************...........................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |************************..........................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |************************..........................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*************************.........................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*************************.........................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**************************........................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**************************........................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***************************.......................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***************************.......................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |****************************......................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |****************************......................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*****************************.....................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*****************************.....................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |******************************....................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |******************************....................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*******************************...................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*******************************...................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |********************************..................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |********************************..................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*********************************.................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*********************************.................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**********************************................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**********************************................| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***********************************...............| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***********************************...............| Elapsed Time: 00:00:13 Batch 34/60, Progress: |************************************..............| Elapsed Time: 00:00:13 Batch 34/60, Progress: |************************************..............| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*************************************.............| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*************************************.............| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**************************************............| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**************************************............| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***************************************...........| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***************************************...........| Elapsed Time: 00:00:13 Batch 34/60, Progress: |****************************************..........| Elapsed Time: 00:00:13 Batch 34/60, Progress: |****************************************..........| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*****************************************.........| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*****************************************.........| Elapsed Time: 00:00:13 Batch 34/60, Progress: |******************************************........| Elapsed Time: 00:00:13 Batch 34/60, Progress: |******************************************........| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*******************************************.......| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*******************************************.......| Elapsed Time: 00:00:13 Batch 34/60, Progress: |********************************************......| Elapsed Time: 00:00:13 Batch 34/60, Progress: |********************************************......| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*********************************************.....| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*********************************************.....| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**********************************************....| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**********************************************....| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***********************************************...| Elapsed Time: 00:00:13 Batch 34/60, Progress: |***********************************************...| Elapsed Time: 00:00:13 Batch 34/60, Progress: |************************************************..| Elapsed Time: 00:00:13 Batch 34/60, Progress: |************************************************..| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*************************************************.| Elapsed Time: 00:00:13 Batch 34/60, Progress: |*************************************************.| Elapsed Time: 00:00:13 Batch 34/60, Progress: |**************************************************| Elapsed Time: 00:00:13 
#> Batch 35/60, Progress: |..................................................| Elapsed Time: 00:00:13 Batch 35/60, Progress: |..................................................| Elapsed Time: 00:00:13 Batch 35/60, Progress: |*.................................................| Elapsed Time: 00:00:13 Batch 35/60, Progress: |*.................................................| Elapsed Time: 00:00:13 Batch 35/60, Progress: |**................................................| Elapsed Time: 00:00:13 Batch 35/60, Progress: |**................................................| Elapsed Time: 00:00:13 Batch 35/60, Progress: |***...............................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***...............................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |****..............................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |****..............................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*****.............................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*****.............................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |******............................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |******............................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*******...........................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*******...........................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |********..........................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |********..........................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*********.........................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*********.........................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**********........................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**********........................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***********.......................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***********.......................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |************......................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |************......................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*************.....................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*************.....................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**************....................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**************....................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***************...................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***************...................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |****************..................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |****************..................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*****************.................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*****************.................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |******************................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |******************................................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*******************...............................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*******************...............................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |********************..............................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |********************..............................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*********************.............................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*********************.............................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**********************............................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**********************............................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***********************...........................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***********************...........................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |************************..........................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |************************..........................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*************************.........................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*************************.........................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**************************........................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**************************........................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***************************.......................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***************************.......................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |****************************......................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |****************************......................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*****************************.....................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*****************************.....................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |******************************....................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |******************************....................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*******************************...................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*******************************...................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |********************************..................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |********************************..................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*********************************.................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*********************************.................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**********************************................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**********************************................| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***********************************...............| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***********************************...............| Elapsed Time: 00:00:14 Batch 35/60, Progress: |************************************..............| Elapsed Time: 00:00:14 Batch 35/60, Progress: |************************************..............| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*************************************.............| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*************************************.............| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**************************************............| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**************************************............| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***************************************...........| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***************************************...........| Elapsed Time: 00:00:14 Batch 35/60, Progress: |****************************************..........| Elapsed Time: 00:00:14 Batch 35/60, Progress: |****************************************..........| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*****************************************.........| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*****************************************.........| Elapsed Time: 00:00:14 Batch 35/60, Progress: |******************************************........| Elapsed Time: 00:00:14 Batch 35/60, Progress: |******************************************........| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*******************************************.......| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*******************************************.......| Elapsed Time: 00:00:14 Batch 35/60, Progress: |********************************************......| Elapsed Time: 00:00:14 Batch 35/60, Progress: |********************************************......| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*********************************************.....| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*********************************************.....| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**********************************************....| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**********************************************....| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***********************************************...| Elapsed Time: 00:00:14 Batch 35/60, Progress: |***********************************************...| Elapsed Time: 00:00:14 Batch 35/60, Progress: |************************************************..| Elapsed Time: 00:00:14 Batch 35/60, Progress: |************************************************..| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*************************************************.| Elapsed Time: 00:00:14 Batch 35/60, Progress: |*************************************************.| Elapsed Time: 00:00:14 Batch 35/60, Progress: |**************************************************| Elapsed Time: 00:00:14 
#> Batch 36/60, Progress: |..................................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |..................................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*.................................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*.................................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**................................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**................................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***...............................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***...............................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |****..............................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |****..............................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*****.............................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*****.............................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |******............................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |******............................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*******...........................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*******...........................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |********..........................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |********..........................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*********.........................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*********.........................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**********........................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**********........................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***********.......................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***********.......................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |************......................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |************......................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*************.....................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*************.....................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**************....................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**************....................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***************...................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***************...................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |****************..................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |****************..................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*****************.................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*****************.................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |******************................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |******************................................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*******************...............................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*******************...............................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |********************..............................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |********************..............................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*********************.............................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*********************.............................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**********************............................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**********************............................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***********************...........................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***********************...........................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |************************..........................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |************************..........................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*************************.........................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*************************.........................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**************************........................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**************************........................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***************************.......................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***************************.......................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |****************************......................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |****************************......................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*****************************.....................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*****************************.....................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |******************************....................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |******************************....................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*******************************...................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*******************************...................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |********************************..................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |********************************..................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*********************************.................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*********************************.................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**********************************................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**********************************................| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***********************************...............| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***********************************...............| Elapsed Time: 00:00:14 Batch 36/60, Progress: |************************************..............| Elapsed Time: 00:00:14 Batch 36/60, Progress: |************************************..............| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*************************************.............| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*************************************.............| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**************************************............| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**************************************............| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***************************************...........| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***************************************...........| Elapsed Time: 00:00:14 Batch 36/60, Progress: |****************************************..........| Elapsed Time: 00:00:14 Batch 36/60, Progress: |****************************************..........| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*****************************************.........| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*****************************************.........| Elapsed Time: 00:00:14 Batch 36/60, Progress: |******************************************........| Elapsed Time: 00:00:14 Batch 36/60, Progress: |******************************************........| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*******************************************.......| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*******************************************.......| Elapsed Time: 00:00:14 Batch 36/60, Progress: |********************************************......| Elapsed Time: 00:00:14 Batch 36/60, Progress: |********************************************......| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*********************************************.....| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*********************************************.....| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**********************************************....| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**********************************************....| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***********************************************...| Elapsed Time: 00:00:14 Batch 36/60, Progress: |***********************************************...| Elapsed Time: 00:00:14 Batch 36/60, Progress: |************************************************..| Elapsed Time: 00:00:14 Batch 36/60, Progress: |************************************************..| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*************************************************.| Elapsed Time: 00:00:14 Batch 36/60, Progress: |*************************************************.| Elapsed Time: 00:00:14 Batch 36/60, Progress: |**************************************************| Elapsed Time: 00:00:14 
#> Batch 37/60, Progress: |..................................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |..................................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*.................................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*.................................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**................................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**................................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***...............................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***...............................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |****..............................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |****..............................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*****.............................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*****.............................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |******............................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |******............................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*******...........................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*******...........................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |********..........................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |********..........................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*********.........................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*********.........................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**********........................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**********........................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***********.......................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***********.......................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |************......................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |************......................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*************.....................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*************.....................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**************....................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**************....................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***************...................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***************...................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |****************..................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |****************..................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*****************.................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*****************.................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |******************................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |******************................................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*******************...............................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*******************...............................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |********************..............................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |********************..............................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*********************.............................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*********************.............................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**********************............................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**********************............................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***********************...........................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***********************...........................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |************************..........................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |************************..........................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*************************.........................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*************************.........................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**************************........................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**************************........................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***************************.......................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |***************************.......................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |****************************......................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |****************************......................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*****************************.....................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*****************************.....................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |******************************....................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |******************************....................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*******************************...................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*******************************...................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |********************************..................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |********************************..................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*********************************.................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |*********************************.................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**********************************................| Elapsed Time: 00:00:14 Batch 37/60, Progress: |**********************************................| Elapsed Time: 00:00:15 Batch 37/60, Progress: |***********************************...............| Elapsed Time: 00:00:15 Batch 37/60, Progress: |***********************************...............| Elapsed Time: 00:00:15 Batch 37/60, Progress: |************************************..............| Elapsed Time: 00:00:15 Batch 37/60, Progress: |************************************..............| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*************************************.............| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*************************************.............| Elapsed Time: 00:00:15 Batch 37/60, Progress: |**************************************............| Elapsed Time: 00:00:15 Batch 37/60, Progress: |**************************************............| Elapsed Time: 00:00:15 Batch 37/60, Progress: |***************************************...........| Elapsed Time: 00:00:15 Batch 37/60, Progress: |***************************************...........| Elapsed Time: 00:00:15 Batch 37/60, Progress: |****************************************..........| Elapsed Time: 00:00:15 Batch 37/60, Progress: |****************************************..........| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*****************************************.........| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*****************************************.........| Elapsed Time: 00:00:15 Batch 37/60, Progress: |******************************************........| Elapsed Time: 00:00:15 Batch 37/60, Progress: |******************************************........| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*******************************************.......| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*******************************************.......| Elapsed Time: 00:00:15 Batch 37/60, Progress: |********************************************......| Elapsed Time: 00:00:15 Batch 37/60, Progress: |********************************************......| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*********************************************.....| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*********************************************.....| Elapsed Time: 00:00:15 Batch 37/60, Progress: |**********************************************....| Elapsed Time: 00:00:15 Batch 37/60, Progress: |**********************************************....| Elapsed Time: 00:00:15 Batch 37/60, Progress: |***********************************************...| Elapsed Time: 00:00:15 Batch 37/60, Progress: |***********************************************...| Elapsed Time: 00:00:15 Batch 37/60, Progress: |************************************************..| Elapsed Time: 00:00:15 Batch 37/60, Progress: |************************************************..| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*************************************************.| Elapsed Time: 00:00:15 Batch 37/60, Progress: |*************************************************.| Elapsed Time: 00:00:15 Batch 37/60, Progress: |**************************************************| Elapsed Time: 00:00:15 
#> Batch 38/60, Progress: |..................................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |..................................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*.................................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*.................................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**................................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**................................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***...............................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***...............................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |****..............................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |****..............................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*****.............................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*****.............................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |******............................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |******............................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*******...........................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*******...........................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |********..........................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |********..........................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*********.........................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*********.........................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**********........................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**********........................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***********.......................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***********.......................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |************......................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |************......................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*************.....................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*************.....................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**************....................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**************....................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***************...................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***************...................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |****************..................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |****************..................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*****************.................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*****************.................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |******************................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |******************................................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*******************...............................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*******************...............................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |********************..............................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |********************..............................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*********************.............................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*********************.............................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**********************............................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**********************............................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***********************...........................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***********************...........................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |************************..........................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |************************..........................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*************************.........................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*************************.........................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**************************........................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**************************........................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***************************.......................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***************************.......................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |****************************......................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |****************************......................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*****************************.....................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*****************************.....................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |******************************....................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |******************************....................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*******************************...................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*******************************...................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |********************************..................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |********************************..................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*********************************.................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*********************************.................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**********************************................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**********************************................| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***********************************...............| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***********************************...............| Elapsed Time: 00:00:15 Batch 38/60, Progress: |************************************..............| Elapsed Time: 00:00:15 Batch 38/60, Progress: |************************************..............| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*************************************.............| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*************************************.............| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**************************************............| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**************************************............| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***************************************...........| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***************************************...........| Elapsed Time: 00:00:15 Batch 38/60, Progress: |****************************************..........| Elapsed Time: 00:00:15 Batch 38/60, Progress: |****************************************..........| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*****************************************.........| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*****************************************.........| Elapsed Time: 00:00:15 Batch 38/60, Progress: |******************************************........| Elapsed Time: 00:00:15 Batch 38/60, Progress: |******************************************........| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*******************************************.......| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*******************************************.......| Elapsed Time: 00:00:15 Batch 38/60, Progress: |********************************************......| Elapsed Time: 00:00:15 Batch 38/60, Progress: |********************************************......| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*********************************************.....| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*********************************************.....| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**********************************************....| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**********************************************....| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***********************************************...| Elapsed Time: 00:00:15 Batch 38/60, Progress: |***********************************************...| Elapsed Time: 00:00:15 Batch 38/60, Progress: |************************************************..| Elapsed Time: 00:00:15 Batch 38/60, Progress: |************************************************..| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*************************************************.| Elapsed Time: 00:00:15 Batch 38/60, Progress: |*************************************************.| Elapsed Time: 00:00:15 Batch 38/60, Progress: |**************************************************| Elapsed Time: 00:00:15 
#> Batch 39/60, Progress: |..................................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |..................................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*.................................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*.................................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**................................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**................................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***...............................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***...............................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |****..............................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |****..............................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*****.............................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*****.............................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |******............................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |******............................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*******...........................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*******...........................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |********..........................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |********..........................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*********.........................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*********.........................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**********........................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**********........................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***********.......................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***********.......................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |************......................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |************......................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*************.....................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*************.....................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**************....................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**************....................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***************...................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***************...................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |****************..................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |****************..................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*****************.................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*****************.................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |******************................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |******************................................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*******************...............................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*******************...............................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |********************..............................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |********************..............................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*********************.............................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*********************.............................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**********************............................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**********************............................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***********************...........................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***********************...........................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |************************..........................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |************************..........................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*************************.........................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*************************.........................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**************************........................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**************************........................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***************************.......................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***************************.......................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |****************************......................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |****************************......................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*****************************.....................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*****************************.....................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |******************************....................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |******************************....................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*******************************...................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*******************************...................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |********************************..................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |********************************..................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*********************************.................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*********************************.................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**********************************................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**********************************................| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***********************************...............| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***********************************...............| Elapsed Time: 00:00:15 Batch 39/60, Progress: |************************************..............| Elapsed Time: 00:00:15 Batch 39/60, Progress: |************************************..............| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*************************************.............| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*************************************.............| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**************************************............| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**************************************............| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***************************************...........| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***************************************...........| Elapsed Time: 00:00:15 Batch 39/60, Progress: |****************************************..........| Elapsed Time: 00:00:15 Batch 39/60, Progress: |****************************************..........| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*****************************************.........| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*****************************************.........| Elapsed Time: 00:00:15 Batch 39/60, Progress: |******************************************........| Elapsed Time: 00:00:15 Batch 39/60, Progress: |******************************************........| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*******************************************.......| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*******************************************.......| Elapsed Time: 00:00:15 Batch 39/60, Progress: |********************************************......| Elapsed Time: 00:00:15 Batch 39/60, Progress: |********************************************......| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*********************************************.....| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*********************************************.....| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**********************************************....| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**********************************************....| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***********************************************...| Elapsed Time: 00:00:15 Batch 39/60, Progress: |***********************************************...| Elapsed Time: 00:00:15 Batch 39/60, Progress: |************************************************..| Elapsed Time: 00:00:15 Batch 39/60, Progress: |************************************************..| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*************************************************.| Elapsed Time: 00:00:15 Batch 39/60, Progress: |*************************************************.| Elapsed Time: 00:00:15 Batch 39/60, Progress: |**************************************************| Elapsed Time: 00:00:15 
#> Batch 40/60, Progress: |..................................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |..................................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*.................................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*.................................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**................................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**................................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***...............................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***...............................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |****..............................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |****..............................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*****.............................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*****.............................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |******............................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |******............................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*******...........................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*******...........................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |********..........................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |********..........................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*********.........................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*********.........................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**********........................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**********........................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***********.......................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***********.......................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |************......................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |************......................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*************.....................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*************.....................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**************....................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**************....................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***************...................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***************...................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |****************..................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |****************..................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*****************.................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*****************.................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |******************................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |******************................................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*******************...............................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*******************...............................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |********************..............................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |********************..............................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*********************.............................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*********************.............................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**********************............................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**********************............................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***********************...........................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***********************...........................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |************************..........................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |************************..........................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*************************.........................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*************************.........................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**************************........................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**************************........................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***************************.......................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***************************.......................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |****************************......................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |****************************......................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*****************************.....................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*****************************.....................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |******************************....................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |******************************....................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*******************************...................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*******************************...................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |********************************..................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |********************************..................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*********************************.................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*********************************.................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**********************************................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**********************************................| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***********************************...............| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***********************************...............| Elapsed Time: 00:00:16 Batch 40/60, Progress: |************************************..............| Elapsed Time: 00:00:16 Batch 40/60, Progress: |************************************..............| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*************************************.............| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*************************************.............| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**************************************............| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**************************************............| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***************************************...........| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***************************************...........| Elapsed Time: 00:00:16 Batch 40/60, Progress: |****************************************..........| Elapsed Time: 00:00:16 Batch 40/60, Progress: |****************************************..........| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*****************************************.........| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*****************************************.........| Elapsed Time: 00:00:16 Batch 40/60, Progress: |******************************************........| Elapsed Time: 00:00:16 Batch 40/60, Progress: |******************************************........| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*******************************************.......| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*******************************************.......| Elapsed Time: 00:00:16 Batch 40/60, Progress: |********************************************......| Elapsed Time: 00:00:16 Batch 40/60, Progress: |********************************************......| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*********************************************.....| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*********************************************.....| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**********************************************....| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**********************************************....| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***********************************************...| Elapsed Time: 00:00:16 Batch 40/60, Progress: |***********************************************...| Elapsed Time: 00:00:16 Batch 40/60, Progress: |************************************************..| Elapsed Time: 00:00:16 Batch 40/60, Progress: |************************************************..| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*************************************************.| Elapsed Time: 00:00:16 Batch 40/60, Progress: |*************************************************.| Elapsed Time: 00:00:16 Batch 40/60, Progress: |**************************************************| Elapsed Time: 00:00:16 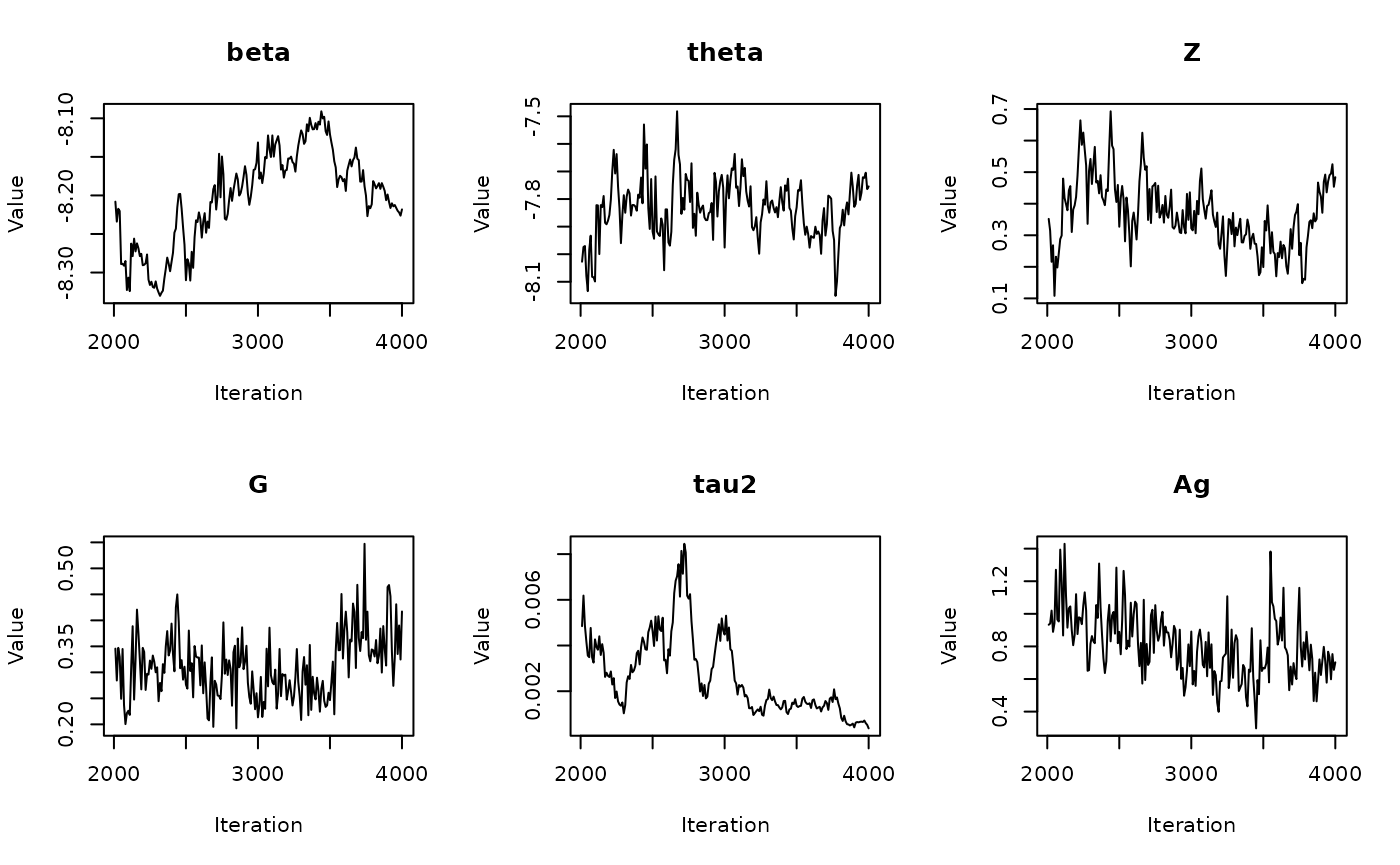
#> Batch 41/60, Progress: |..................................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |..................................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*.................................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*.................................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**................................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**................................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***...............................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***...............................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |****..............................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |****..............................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*****.............................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*****.............................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |******............................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |******............................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*******...........................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*******...........................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |********..........................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |********..........................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*********.........................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*********.........................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**********........................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**********........................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***********.......................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***********.......................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |************......................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |************......................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*************.....................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*************.....................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**************....................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**************....................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***************...................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***************...................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |****************..................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |****************..................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*****************.................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*****************.................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |******************................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |******************................................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*******************...............................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*******************...............................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |********************..............................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |********************..............................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*********************.............................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*********************.............................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**********************............................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**********************............................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***********************...........................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***********************...........................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |************************..........................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |************************..........................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*************************.........................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*************************.........................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**************************........................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**************************........................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***************************.......................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***************************.......................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |****************************......................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |****************************......................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*****************************.....................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*****************************.....................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |******************************....................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |******************************....................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*******************************...................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*******************************...................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |********************************..................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |********************************..................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*********************************.................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*********************************.................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**********************************................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**********************************................| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***********************************...............| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***********************************...............| Elapsed Time: 00:00:16 Batch 41/60, Progress: |************************************..............| Elapsed Time: 00:00:16 Batch 41/60, Progress: |************************************..............| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*************************************.............| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*************************************.............| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**************************************............| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**************************************............| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***************************************...........| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***************************************...........| Elapsed Time: 00:00:16 Batch 41/60, Progress: |****************************************..........| Elapsed Time: 00:00:16 Batch 41/60, Progress: |****************************************..........| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*****************************************.........| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*****************************************.........| Elapsed Time: 00:00:16 Batch 41/60, Progress: |******************************************........| Elapsed Time: 00:00:16 Batch 41/60, Progress: |******************************************........| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*******************************************.......| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*******************************************.......| Elapsed Time: 00:00:16 Batch 41/60, Progress: |********************************************......| Elapsed Time: 00:00:16 Batch 41/60, Progress: |********************************************......| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*********************************************.....| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*********************************************.....| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**********************************************....| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**********************************************....| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***********************************************...| Elapsed Time: 00:00:16 Batch 41/60, Progress: |***********************************************...| Elapsed Time: 00:00:16 Batch 41/60, Progress: |************************************************..| Elapsed Time: 00:00:16 Batch 41/60, Progress: |************************************************..| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*************************************************.| Elapsed Time: 00:00:16 Batch 41/60, Progress: |*************************************************.| Elapsed Time: 00:00:16 Batch 41/60, Progress: |**************************************************| Elapsed Time: 00:00:16 
#> Batch 42/60, Progress: |..................................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |..................................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*.................................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*.................................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |**................................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |**................................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |***...............................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |***...............................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |****..............................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |****..............................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*****.............................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*****.............................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |******............................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |******............................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*******...........................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*******...........................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |********..........................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |********..........................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*********.........................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*********.........................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |**********........................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |**********........................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |***********.......................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |***********.......................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |************......................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |************......................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*************.....................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*************.....................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |**************....................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |**************....................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |***************...................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |***************...................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |****************..................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |****************..................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*****************.................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*****************.................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |******************................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |******************................................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*******************...............................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*******************...............................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |********************..............................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |********************..............................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*********************.............................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*********************.............................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |**********************............................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |**********************............................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |***********************...........................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |***********************...........................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |************************..........................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |************************..........................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*************************.........................| Elapsed Time: 00:00:16 Batch 42/60, Progress: |*************************.........................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |**************************........................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |**************************........................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |***************************.......................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |***************************.......................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |****************************......................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |****************************......................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*****************************.....................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*****************************.....................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |******************************....................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |******************************....................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*******************************...................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*******************************...................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |********************************..................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |********************************..................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*********************************.................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*********************************.................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |**********************************................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |**********************************................| Elapsed Time: 00:00:17 Batch 42/60, Progress: |***********************************...............| Elapsed Time: 00:00:17 Batch 42/60, Progress: |***********************************...............| Elapsed Time: 00:00:17 Batch 42/60, Progress: |************************************..............| Elapsed Time: 00:00:17 Batch 42/60, Progress: |************************************..............| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*************************************.............| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*************************************.............| Elapsed Time: 00:00:17 Batch 42/60, Progress: |**************************************............| Elapsed Time: 00:00:17 Batch 42/60, Progress: |**************************************............| Elapsed Time: 00:00:17 Batch 42/60, Progress: |***************************************...........| Elapsed Time: 00:00:17 Batch 42/60, Progress: |***************************************...........| Elapsed Time: 00:00:17 Batch 42/60, Progress: |****************************************..........| Elapsed Time: 00:00:17 Batch 42/60, Progress: |****************************************..........| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*****************************************.........| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*****************************************.........| Elapsed Time: 00:00:17 Batch 42/60, Progress: |******************************************........| Elapsed Time: 00:00:17 Batch 42/60, Progress: |******************************************........| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*******************************************.......| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*******************************************.......| Elapsed Time: 00:00:17 Batch 42/60, Progress: |********************************************......| Elapsed Time: 00:00:17 Batch 42/60, Progress: |********************************************......| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*********************************************.....| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*********************************************.....| Elapsed Time: 00:00:17 Batch 42/60, Progress: |**********************************************....| Elapsed Time: 00:00:17 Batch 42/60, Progress: |**********************************************....| Elapsed Time: 00:00:17 Batch 42/60, Progress: |***********************************************...| Elapsed Time: 00:00:17 Batch 42/60, Progress: |***********************************************...| Elapsed Time: 00:00:17 Batch 42/60, Progress: |************************************************..| Elapsed Time: 00:00:17 Batch 42/60, Progress: |************************************************..| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*************************************************.| Elapsed Time: 00:00:17 Batch 42/60, Progress: |*************************************************.| Elapsed Time: 00:00:17 Batch 42/60, Progress: |**************************************************| Elapsed Time: 00:00:17 
#> Batch 43/60, Progress: |..................................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |..................................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*.................................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*.................................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**................................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**................................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***...............................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***...............................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |****..............................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |****..............................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*****.............................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*****.............................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |******............................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |******............................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*******...........................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*******...........................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |********..........................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |********..........................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*********.........................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*********.........................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**********........................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**********........................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***********.......................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***********.......................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |************......................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |************......................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*************.....................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*************.....................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**************....................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**************....................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***************...................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***************...................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |****************..................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |****************..................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*****************.................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*****************.................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |******************................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |******************................................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*******************...............................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*******************...............................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |********************..............................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |********************..............................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*********************.............................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*********************.............................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**********************............................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**********************............................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***********************...........................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***********************...........................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |************************..........................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |************************..........................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*************************.........................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*************************.........................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**************************........................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**************************........................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***************************.......................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***************************.......................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |****************************......................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |****************************......................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*****************************.....................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*****************************.....................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |******************************....................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |******************************....................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*******************************...................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*******************************...................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |********************************..................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |********************************..................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*********************************.................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*********************************.................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**********************************................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**********************************................| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***********************************...............| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***********************************...............| Elapsed Time: 00:00:17 Batch 43/60, Progress: |************************************..............| Elapsed Time: 00:00:17 Batch 43/60, Progress: |************************************..............| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*************************************.............| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*************************************.............| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**************************************............| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**************************************............| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***************************************...........| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***************************************...........| Elapsed Time: 00:00:17 Batch 43/60, Progress: |****************************************..........| Elapsed Time: 00:00:17 Batch 43/60, Progress: |****************************************..........| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*****************************************.........| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*****************************************.........| Elapsed Time: 00:00:17 Batch 43/60, Progress: |******************************************........| Elapsed Time: 00:00:17 Batch 43/60, Progress: |******************************************........| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*******************************************.......| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*******************************************.......| Elapsed Time: 00:00:17 Batch 43/60, Progress: |********************************************......| Elapsed Time: 00:00:17 Batch 43/60, Progress: |********************************************......| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*********************************************.....| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*********************************************.....| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**********************************************....| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**********************************************....| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***********************************************...| Elapsed Time: 00:00:17 Batch 43/60, Progress: |***********************************************...| Elapsed Time: 00:00:17 Batch 43/60, Progress: |************************************************..| Elapsed Time: 00:00:17 Batch 43/60, Progress: |************************************************..| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*************************************************.| Elapsed Time: 00:00:17 Batch 43/60, Progress: |*************************************************.| Elapsed Time: 00:00:17 Batch 43/60, Progress: |**************************************************| Elapsed Time: 00:00:17 
#> Batch 44/60, Progress: |..................................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |..................................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*.................................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*.................................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**................................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**................................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***...............................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***...............................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |****..............................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |****..............................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*****.............................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*****.............................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |******............................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |******............................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*******...........................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*******...........................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |********..........................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |********..........................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*********.........................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*********.........................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**********........................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**********........................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***********.......................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***********.......................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |************......................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |************......................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*************.....................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*************.....................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**************....................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**************....................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***************...................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***************...................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |****************..................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |****************..................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*****************.................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*****************.................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |******************................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |******************................................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*******************...............................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*******************...............................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |********************..............................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |********************..............................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*********************.............................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*********************.............................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**********************............................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**********************............................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***********************...........................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***********************...........................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |************************..........................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |************************..........................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*************************.........................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*************************.........................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**************************........................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**************************........................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***************************.......................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***************************.......................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |****************************......................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |****************************......................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*****************************.....................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*****************************.....................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |******************************....................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |******************************....................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*******************************...................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*******************************...................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |********************************..................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |********************************..................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*********************************.................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*********************************.................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**********************************................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**********************************................| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***********************************...............| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***********************************...............| Elapsed Time: 00:00:17 Batch 44/60, Progress: |************************************..............| Elapsed Time: 00:00:17 Batch 44/60, Progress: |************************************..............| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*************************************.............| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*************************************.............| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**************************************............| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**************************************............| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***************************************...........| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***************************************...........| Elapsed Time: 00:00:17 Batch 44/60, Progress: |****************************************..........| Elapsed Time: 00:00:17 Batch 44/60, Progress: |****************************************..........| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*****************************************.........| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*****************************************.........| Elapsed Time: 00:00:17 Batch 44/60, Progress: |******************************************........| Elapsed Time: 00:00:17 Batch 44/60, Progress: |******************************************........| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*******************************************.......| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*******************************************.......| Elapsed Time: 00:00:17 Batch 44/60, Progress: |********************************************......| Elapsed Time: 00:00:17 Batch 44/60, Progress: |********************************************......| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*********************************************.....| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*********************************************.....| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**********************************************....| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**********************************************....| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***********************************************...| Elapsed Time: 00:00:17 Batch 44/60, Progress: |***********************************************...| Elapsed Time: 00:00:17 Batch 44/60, Progress: |************************************************..| Elapsed Time: 00:00:17 Batch 44/60, Progress: |************************************************..| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*************************************************.| Elapsed Time: 00:00:17 Batch 44/60, Progress: |*************************************************.| Elapsed Time: 00:00:17 Batch 44/60, Progress: |**************************************************| Elapsed Time: 00:00:17 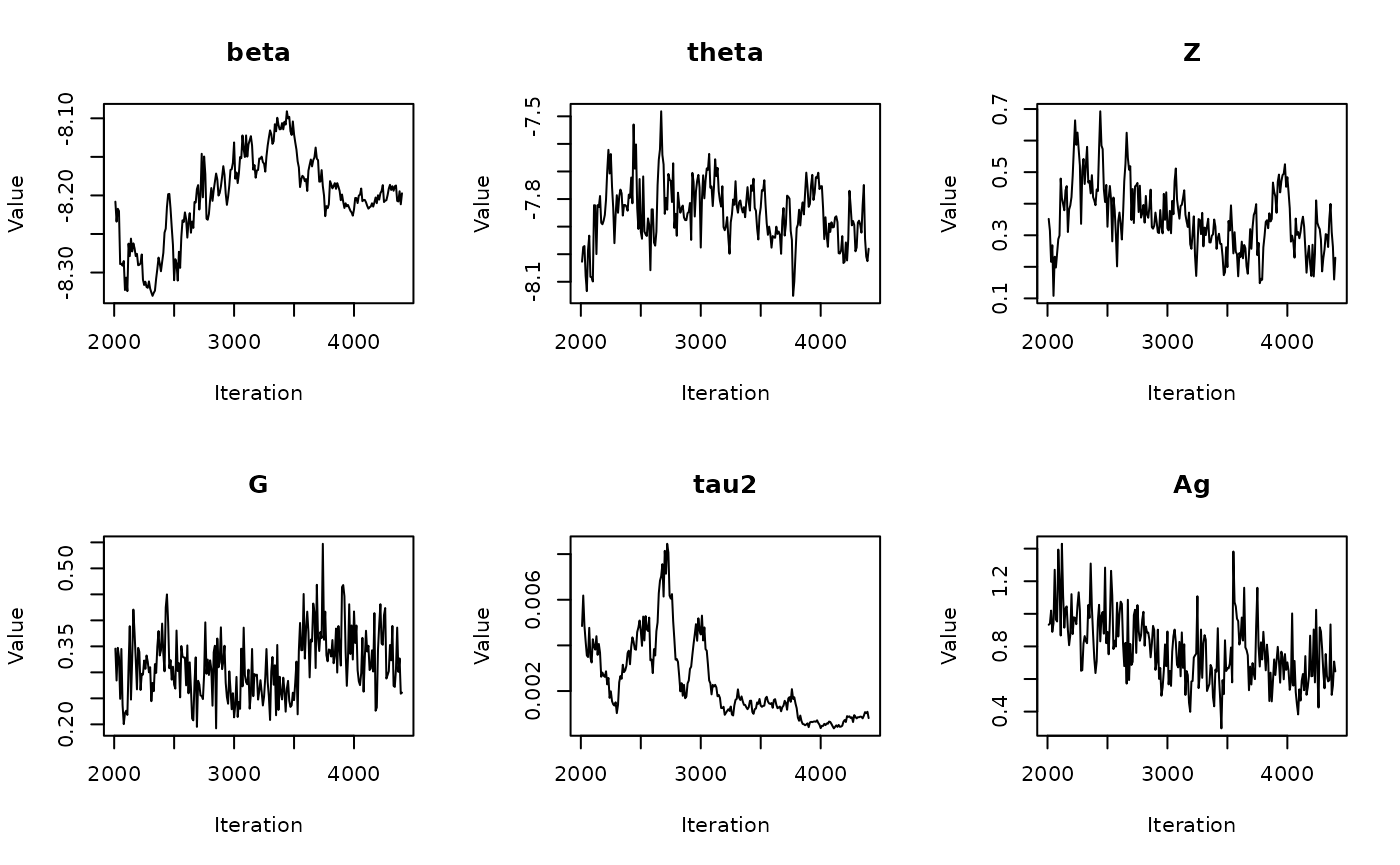
#> Batch 45/60, Progress: |..................................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |..................................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*.................................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*.................................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**................................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**................................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***...............................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***...............................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |****..............................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |****..............................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*****.............................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*****.............................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |******............................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |******............................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*******...........................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*******...........................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |********..........................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |********..........................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*********.........................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*********.........................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**********........................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**********........................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***********.......................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***********.......................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |************......................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |************......................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*************.....................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*************.....................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**************....................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**************....................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***************...................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***************...................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |****************..................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |****************..................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*****************.................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*****************.................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |******************................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |******************................................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*******************...............................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*******************...............................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |********************..............................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |********************..............................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*********************.............................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*********************.............................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**********************............................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**********************............................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***********************...........................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***********************...........................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |************************..........................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |************************..........................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*************************.........................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*************************.........................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**************************........................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**************************........................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***************************.......................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***************************.......................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |****************************......................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |****************************......................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*****************************.....................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*****************************.....................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |******************************....................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |******************************....................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*******************************...................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*******************************...................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |********************************..................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |********************************..................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*********************************.................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*********************************.................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**********************************................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**********************************................| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***********************************...............| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***********************************...............| Elapsed Time: 00:00:18 Batch 45/60, Progress: |************************************..............| Elapsed Time: 00:00:18 Batch 45/60, Progress: |************************************..............| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*************************************.............| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*************************************.............| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**************************************............| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**************************************............| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***************************************...........| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***************************************...........| Elapsed Time: 00:00:18 Batch 45/60, Progress: |****************************************..........| Elapsed Time: 00:00:18 Batch 45/60, Progress: |****************************************..........| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*****************************************.........| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*****************************************.........| Elapsed Time: 00:00:18 Batch 45/60, Progress: |******************************************........| Elapsed Time: 00:00:18 Batch 45/60, Progress: |******************************************........| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*******************************************.......| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*******************************************.......| Elapsed Time: 00:00:18 Batch 45/60, Progress: |********************************************......| Elapsed Time: 00:00:18 Batch 45/60, Progress: |********************************************......| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*********************************************.....| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*********************************************.....| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**********************************************....| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**********************************************....| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***********************************************...| Elapsed Time: 00:00:18 Batch 45/60, Progress: |***********************************************...| Elapsed Time: 00:00:18 Batch 45/60, Progress: |************************************************..| Elapsed Time: 00:00:18 Batch 45/60, Progress: |************************************************..| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*************************************************.| Elapsed Time: 00:00:18 Batch 45/60, Progress: |*************************************************.| Elapsed Time: 00:00:18 Batch 45/60, Progress: |**************************************************| Elapsed Time: 00:00:18 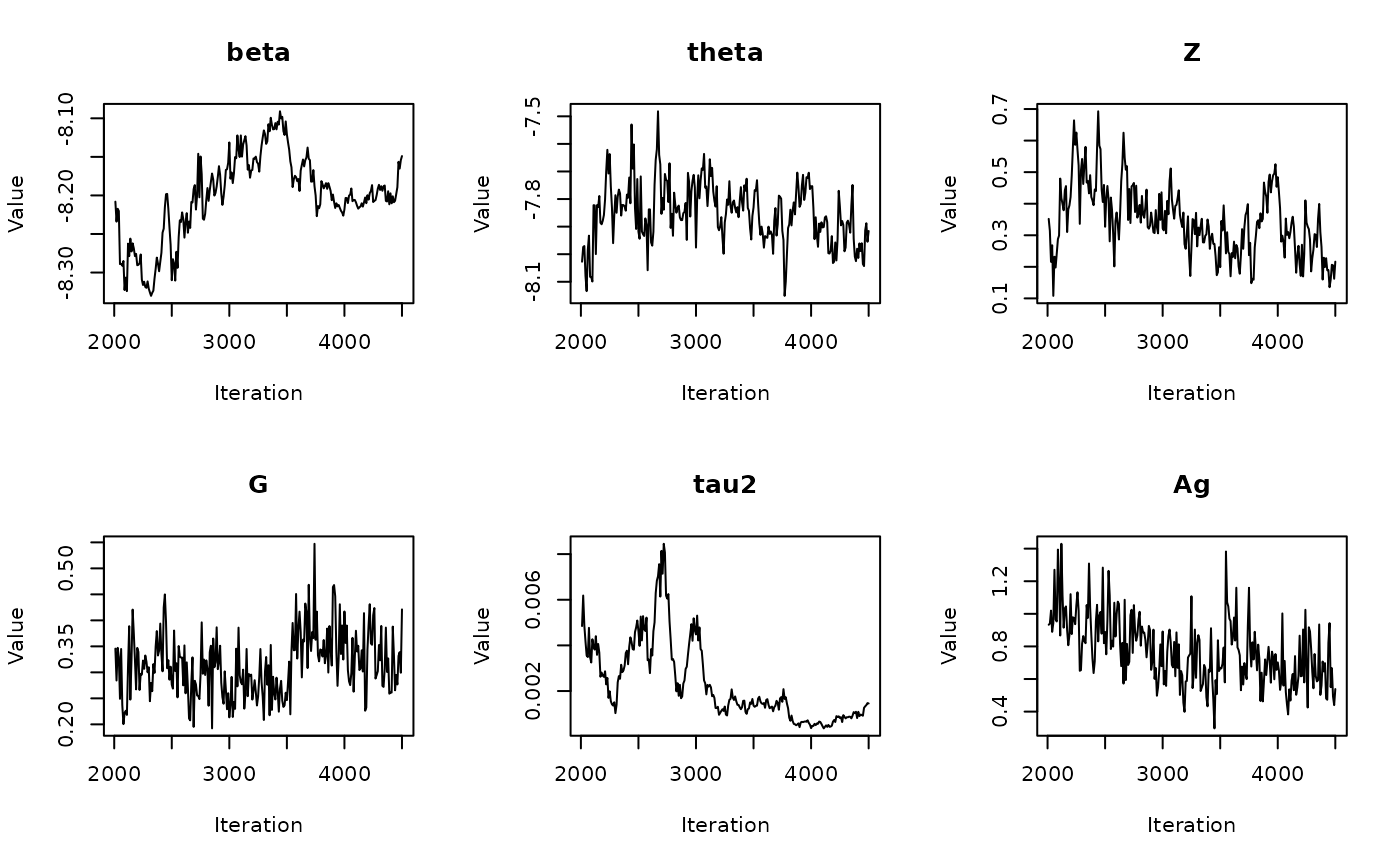
#> Batch 46/60, Progress: |..................................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |..................................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*.................................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*.................................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**................................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**................................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***...............................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***...............................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |****..............................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |****..............................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*****.............................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*****.............................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |******............................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |******............................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*******...........................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*******...........................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |********..........................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |********..........................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*********.........................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*********.........................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**********........................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**********........................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***********.......................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***********.......................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |************......................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |************......................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*************.....................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*************.....................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**************....................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**************....................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***************...................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***************...................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |****************..................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |****************..................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*****************.................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*****************.................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |******************................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |******************................................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*******************...............................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*******************...............................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |********************..............................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |********************..............................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*********************.............................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*********************.............................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**********************............................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**********************............................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***********************...........................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***********************...........................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |************************..........................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |************************..........................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*************************.........................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*************************.........................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**************************........................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**************************........................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***************************.......................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***************************.......................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |****************************......................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |****************************......................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*****************************.....................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*****************************.....................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |******************************....................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |******************************....................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*******************************...................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*******************************...................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |********************************..................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |********************************..................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*********************************.................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*********************************.................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**********************************................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**********************************................| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***********************************...............| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***********************************...............| Elapsed Time: 00:00:18 Batch 46/60, Progress: |************************************..............| Elapsed Time: 00:00:18 Batch 46/60, Progress: |************************************..............| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*************************************.............| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*************************************.............| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**************************************............| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**************************************............| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***************************************...........| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***************************************...........| Elapsed Time: 00:00:18 Batch 46/60, Progress: |****************************************..........| Elapsed Time: 00:00:18 Batch 46/60, Progress: |****************************************..........| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*****************************************.........| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*****************************************.........| Elapsed Time: 00:00:18 Batch 46/60, Progress: |******************************************........| Elapsed Time: 00:00:18 Batch 46/60, Progress: |******************************************........| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*******************************************.......| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*******************************************.......| Elapsed Time: 00:00:18 Batch 46/60, Progress: |********************************************......| Elapsed Time: 00:00:18 Batch 46/60, Progress: |********************************************......| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*********************************************.....| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*********************************************.....| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**********************************************....| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**********************************************....| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***********************************************...| Elapsed Time: 00:00:18 Batch 46/60, Progress: |***********************************************...| Elapsed Time: 00:00:18 Batch 46/60, Progress: |************************************************..| Elapsed Time: 00:00:18 Batch 46/60, Progress: |************************************************..| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*************************************************.| Elapsed Time: 00:00:18 Batch 46/60, Progress: |*************************************************.| Elapsed Time: 00:00:18 Batch 46/60, Progress: |**************************************************| Elapsed Time: 00:00:18 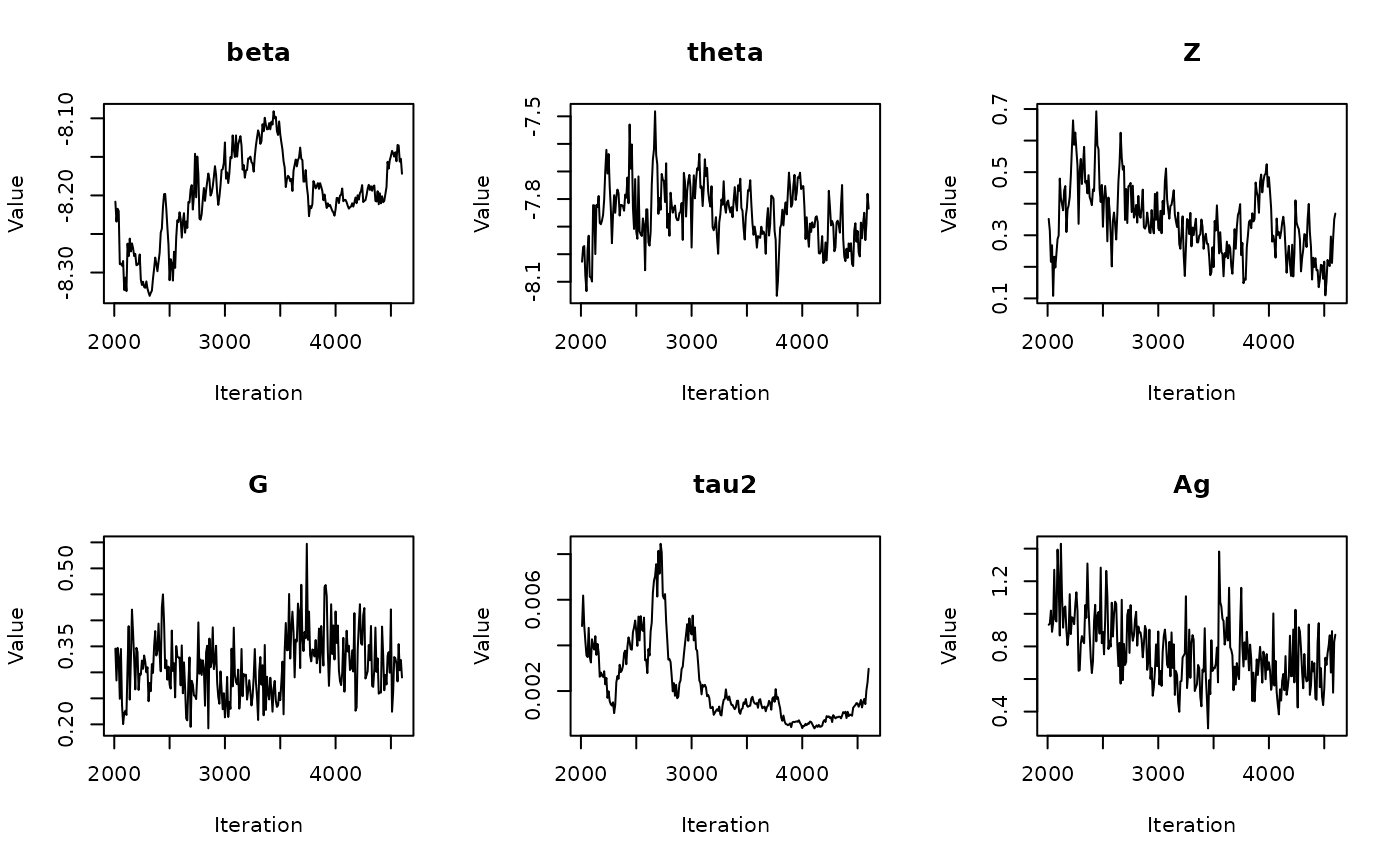
#> Batch 47/60, Progress: |..................................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |..................................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*.................................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*.................................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |**................................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |**................................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |***...............................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |***...............................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |****..............................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |****..............................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*****.............................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*****.............................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |******............................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |******............................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*******...........................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*******...........................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |********..........................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |********..........................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*********.........................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*********.........................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |**********........................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |**********........................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |***********.......................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |***********.......................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |************......................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |************......................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*************.....................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |*************.....................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |**************....................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |**************....................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |***************...................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |***************...................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |****************..................................| Elapsed Time: 00:00:18 Batch 47/60, Progress: |****************..................................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*****************.................................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*****************.................................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |******************................................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |******************................................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*******************...............................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*******************...............................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |********************..............................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |********************..............................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*********************.............................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*********************.............................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**********************............................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**********************............................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***********************...........................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***********************...........................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |************************..........................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |************************..........................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*************************.........................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*************************.........................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**************************........................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**************************........................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***************************.......................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***************************.......................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |****************************......................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |****************************......................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*****************************.....................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*****************************.....................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |******************************....................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |******************************....................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*******************************...................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*******************************...................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |********************************..................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |********************************..................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*********************************.................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*********************************.................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**********************************................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**********************************................| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***********************************...............| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***********************************...............| Elapsed Time: 00:00:19 Batch 47/60, Progress: |************************************..............| Elapsed Time: 00:00:19 Batch 47/60, Progress: |************************************..............| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*************************************.............| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*************************************.............| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**************************************............| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**************************************............| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***************************************...........| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***************************************...........| Elapsed Time: 00:00:19 Batch 47/60, Progress: |****************************************..........| Elapsed Time: 00:00:19 Batch 47/60, Progress: |****************************************..........| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*****************************************.........| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*****************************************.........| Elapsed Time: 00:00:19 Batch 47/60, Progress: |******************************************........| Elapsed Time: 00:00:19 Batch 47/60, Progress: |******************************************........| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*******************************************.......| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*******************************************.......| Elapsed Time: 00:00:19 Batch 47/60, Progress: |********************************************......| Elapsed Time: 00:00:19 Batch 47/60, Progress: |********************************************......| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*********************************************.....| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*********************************************.....| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**********************************************....| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**********************************************....| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***********************************************...| Elapsed Time: 00:00:19 Batch 47/60, Progress: |***********************************************...| Elapsed Time: 00:00:19 Batch 47/60, Progress: |************************************************..| Elapsed Time: 00:00:19 Batch 47/60, Progress: |************************************************..| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*************************************************.| Elapsed Time: 00:00:19 Batch 47/60, Progress: |*************************************************.| Elapsed Time: 00:00:19 Batch 47/60, Progress: |**************************************************| Elapsed Time: 00:00:19 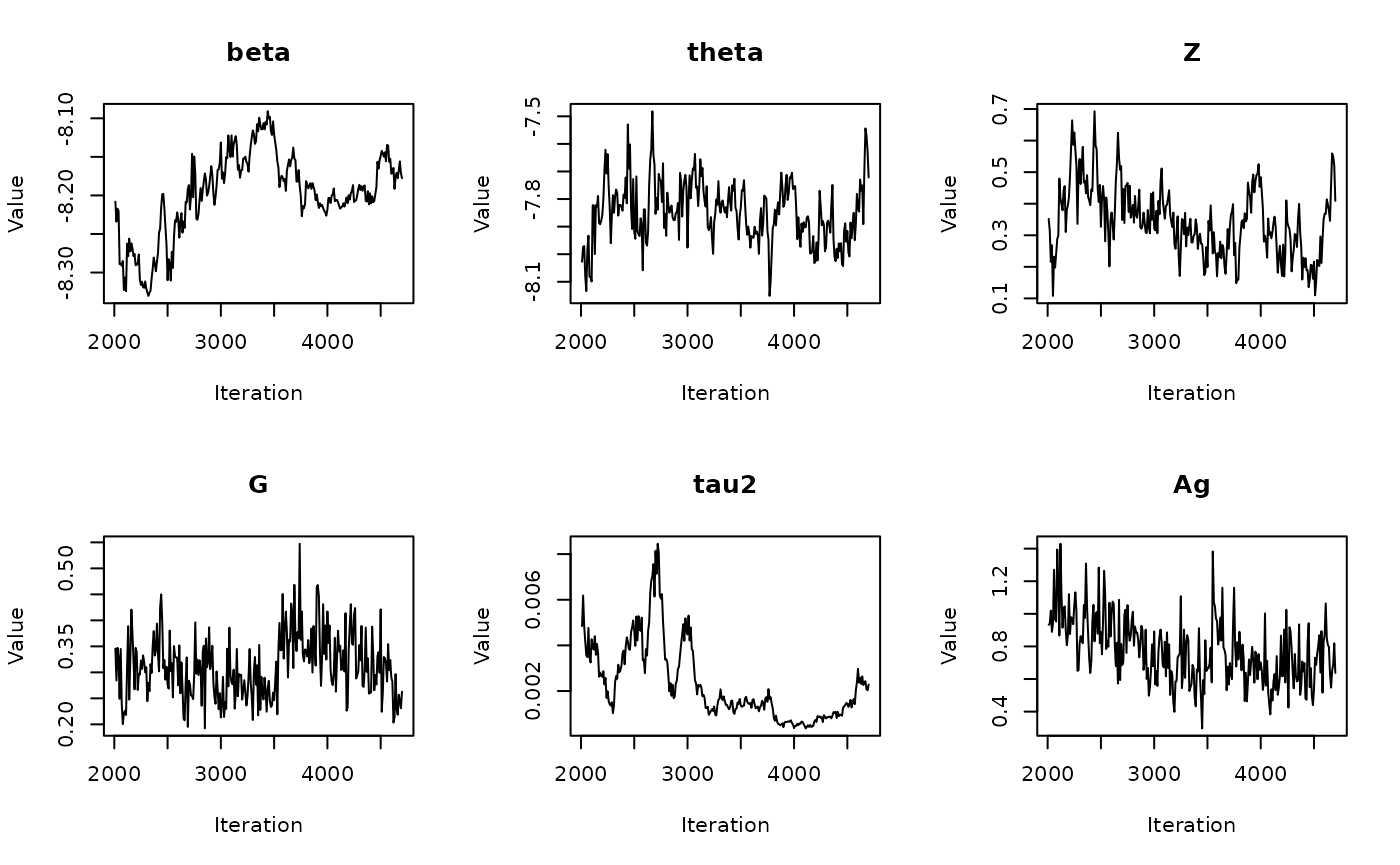
#> Batch 48/60, Progress: |..................................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |..................................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*.................................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*.................................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**................................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**................................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***...............................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***...............................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |****..............................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |****..............................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*****.............................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*****.............................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |******............................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |******............................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*******...........................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*******...........................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |********..........................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |********..........................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*********.........................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*********.........................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**********........................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**********........................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***********.......................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***********.......................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |************......................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |************......................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*************.....................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*************.....................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**************....................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**************....................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***************...................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***************...................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |****************..................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |****************..................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*****************.................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*****************.................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |******************................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |******************................................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*******************...............................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*******************...............................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |********************..............................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |********************..............................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*********************.............................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*********************.............................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**********************............................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**********************............................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***********************...........................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***********************...........................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |************************..........................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |************************..........................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*************************.........................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*************************.........................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**************************........................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**************************........................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***************************.......................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***************************.......................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |****************************......................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |****************************......................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*****************************.....................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*****************************.....................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |******************************....................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |******************************....................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*******************************...................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*******************************...................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |********************************..................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |********************************..................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*********************************.................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*********************************.................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**********************************................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**********************************................| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***********************************...............| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***********************************...............| Elapsed Time: 00:00:19 Batch 48/60, Progress: |************************************..............| Elapsed Time: 00:00:19 Batch 48/60, Progress: |************************************..............| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*************************************.............| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*************************************.............| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**************************************............| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**************************************............| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***************************************...........| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***************************************...........| Elapsed Time: 00:00:19 Batch 48/60, Progress: |****************************************..........| Elapsed Time: 00:00:19 Batch 48/60, Progress: |****************************************..........| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*****************************************.........| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*****************************************.........| Elapsed Time: 00:00:19 Batch 48/60, Progress: |******************************************........| Elapsed Time: 00:00:19 Batch 48/60, Progress: |******************************************........| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*******************************************.......| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*******************************************.......| Elapsed Time: 00:00:19 Batch 48/60, Progress: |********************************************......| Elapsed Time: 00:00:19 Batch 48/60, Progress: |********************************************......| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*********************************************.....| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*********************************************.....| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**********************************************....| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**********************************************....| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***********************************************...| Elapsed Time: 00:00:19 Batch 48/60, Progress: |***********************************************...| Elapsed Time: 00:00:19 Batch 48/60, Progress: |************************************************..| Elapsed Time: 00:00:19 Batch 48/60, Progress: |************************************************..| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*************************************************.| Elapsed Time: 00:00:19 Batch 48/60, Progress: |*************************************************.| Elapsed Time: 00:00:19 Batch 48/60, Progress: |**************************************************| Elapsed Time: 00:00:19 
#> Batch 49/60, Progress: |..................................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |..................................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*.................................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*.................................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**................................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**................................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***...............................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***...............................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |****..............................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |****..............................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*****.............................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*****.............................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |******............................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |******............................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*******...........................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*******...........................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |********..........................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |********..........................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*********.........................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*********.........................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**********........................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**********........................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***********.......................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***********.......................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |************......................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |************......................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*************.....................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*************.....................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**************....................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**************....................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***************...................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***************...................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |****************..................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |****************..................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*****************.................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*****************.................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |******************................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |******************................................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*******************...............................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*******************...............................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |********************..............................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |********************..............................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*********************.............................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*********************.............................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**********************............................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**********************............................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***********************...........................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***********************...........................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |************************..........................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |************************..........................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*************************.........................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*************************.........................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**************************........................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**************************........................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***************************.......................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***************************.......................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |****************************......................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |****************************......................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*****************************.....................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*****************************.....................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |******************************....................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |******************************....................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*******************************...................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*******************************...................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |********************************..................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |********************************..................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*********************************.................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*********************************.................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**********************************................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**********************************................| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***********************************...............| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***********************************...............| Elapsed Time: 00:00:19 Batch 49/60, Progress: |************************************..............| Elapsed Time: 00:00:19 Batch 49/60, Progress: |************************************..............| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*************************************.............| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*************************************.............| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**************************************............| Elapsed Time: 00:00:19 Batch 49/60, Progress: |**************************************............| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***************************************...........| Elapsed Time: 00:00:19 Batch 49/60, Progress: |***************************************...........| Elapsed Time: 00:00:19 Batch 49/60, Progress: |****************************************..........| Elapsed Time: 00:00:19 Batch 49/60, Progress: |****************************************..........| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*****************************************.........| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*****************************************.........| Elapsed Time: 00:00:19 Batch 49/60, Progress: |******************************************........| Elapsed Time: 00:00:19 Batch 49/60, Progress: |******************************************........| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*******************************************.......| Elapsed Time: 00:00:19 Batch 49/60, Progress: |*******************************************.......| Elapsed Time: 00:00:19 Batch 49/60, Progress: |********************************************......| Elapsed Time: 00:00:20 Batch 49/60, Progress: |********************************************......| Elapsed Time: 00:00:20 Batch 49/60, Progress: |*********************************************.....| Elapsed Time: 00:00:20 Batch 49/60, Progress: |*********************************************.....| Elapsed Time: 00:00:20 Batch 49/60, Progress: |**********************************************....| Elapsed Time: 00:00:20 Batch 49/60, Progress: |**********************************************....| Elapsed Time: 00:00:20 Batch 49/60, Progress: |***********************************************...| Elapsed Time: 00:00:20 Batch 49/60, Progress: |***********************************************...| Elapsed Time: 00:00:20 Batch 49/60, Progress: |************************************************..| Elapsed Time: 00:00:20 Batch 49/60, Progress: |************************************************..| Elapsed Time: 00:00:20 Batch 49/60, Progress: |*************************************************.| Elapsed Time: 00:00:20 Batch 49/60, Progress: |*************************************************.| Elapsed Time: 00:00:20 Batch 49/60, Progress: |**************************************************| Elapsed Time: 00:00:20 
#> Batch 50/60, Progress: |..................................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |..................................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*.................................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*.................................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**................................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**................................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***...............................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***...............................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |****..............................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |****..............................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*****.............................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*****.............................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |******............................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |******............................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*******...........................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*******...........................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |********..........................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |********..........................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*********.........................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*********.........................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**********........................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**********........................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***********.......................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***********.......................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |************......................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |************......................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*************.....................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*************.....................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**************....................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**************....................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***************...................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***************...................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |****************..................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |****************..................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*****************.................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*****************.................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |******************................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |******************................................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*******************...............................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*******************...............................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |********************..............................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |********************..............................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*********************.............................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*********************.............................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**********************............................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**********************............................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***********************...........................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***********************...........................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |************************..........................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |************************..........................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*************************.........................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*************************.........................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**************************........................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**************************........................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***************************.......................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***************************.......................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |****************************......................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |****************************......................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*****************************.....................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*****************************.....................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |******************************....................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |******************************....................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*******************************...................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*******************************...................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |********************************..................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |********************************..................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*********************************.................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*********************************.................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**********************************................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**********************************................| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***********************************...............| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***********************************...............| Elapsed Time: 00:00:20 Batch 50/60, Progress: |************************************..............| Elapsed Time: 00:00:20 Batch 50/60, Progress: |************************************..............| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*************************************.............| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*************************************.............| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**************************************............| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**************************************............| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***************************************...........| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***************************************...........| Elapsed Time: 00:00:20 Batch 50/60, Progress: |****************************************..........| Elapsed Time: 00:00:20 Batch 50/60, Progress: |****************************************..........| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*****************************************.........| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*****************************************.........| Elapsed Time: 00:00:20 Batch 50/60, Progress: |******************************************........| Elapsed Time: 00:00:20 Batch 50/60, Progress: |******************************************........| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*******************************************.......| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*******************************************.......| Elapsed Time: 00:00:20 Batch 50/60, Progress: |********************************************......| Elapsed Time: 00:00:20 Batch 50/60, Progress: |********************************************......| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*********************************************.....| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*********************************************.....| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**********************************************....| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**********************************************....| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***********************************************...| Elapsed Time: 00:00:20 Batch 50/60, Progress: |***********************************************...| Elapsed Time: 00:00:20 Batch 50/60, Progress: |************************************************..| Elapsed Time: 00:00:20 Batch 50/60, Progress: |************************************************..| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*************************************************.| Elapsed Time: 00:00:20 Batch 50/60, Progress: |*************************************************.| Elapsed Time: 00:00:20 Batch 50/60, Progress: |**************************************************| Elapsed Time: 00:00:20 
#> Batch 51/60, Progress: |..................................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |..................................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*.................................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*.................................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**................................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**................................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***...............................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***...............................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |****..............................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |****..............................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*****.............................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*****.............................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |******............................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |******............................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*******...........................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*******...........................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |********..........................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |********..........................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*********.........................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*********.........................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**********........................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**********........................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***********.......................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***********.......................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |************......................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |************......................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*************.....................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*************.....................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**************....................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**************....................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***************...................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***************...................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |****************..................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |****************..................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*****************.................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*****************.................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |******************................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |******************................................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*******************...............................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*******************...............................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |********************..............................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |********************..............................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*********************.............................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*********************.............................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**********************............................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**********************............................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***********************...........................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***********************...........................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |************************..........................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |************************..........................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*************************.........................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*************************.........................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**************************........................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**************************........................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***************************.......................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***************************.......................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |****************************......................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |****************************......................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*****************************.....................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*****************************.....................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |******************************....................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |******************************....................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*******************************...................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*******************************...................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |********************************..................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |********************************..................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*********************************.................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*********************************.................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**********************************................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**********************************................| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***********************************...............| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***********************************...............| Elapsed Time: 00:00:20 Batch 51/60, Progress: |************************************..............| Elapsed Time: 00:00:20 Batch 51/60, Progress: |************************************..............| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*************************************.............| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*************************************.............| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**************************************............| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**************************************............| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***************************************...........| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***************************************...........| Elapsed Time: 00:00:20 Batch 51/60, Progress: |****************************************..........| Elapsed Time: 00:00:20 Batch 51/60, Progress: |****************************************..........| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*****************************************.........| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*****************************************.........| Elapsed Time: 00:00:20 Batch 51/60, Progress: |******************************************........| Elapsed Time: 00:00:20 Batch 51/60, Progress: |******************************************........| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*******************************************.......| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*******************************************.......| Elapsed Time: 00:00:20 Batch 51/60, Progress: |********************************************......| Elapsed Time: 00:00:20 Batch 51/60, Progress: |********************************************......| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*********************************************.....| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*********************************************.....| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**********************************************....| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**********************************************....| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***********************************************...| Elapsed Time: 00:00:20 Batch 51/60, Progress: |***********************************************...| Elapsed Time: 00:00:20 Batch 51/60, Progress: |************************************************..| Elapsed Time: 00:00:20 Batch 51/60, Progress: |************************************************..| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*************************************************.| Elapsed Time: 00:00:20 Batch 51/60, Progress: |*************************************************.| Elapsed Time: 00:00:20 Batch 51/60, Progress: |**************************************************| Elapsed Time: 00:00:20 
#> Batch 52/60, Progress: |..................................................| Elapsed Time: 00:00:20 Batch 52/60, Progress: |..................................................| Elapsed Time: 00:00:20 Batch 52/60, Progress: |*.................................................| Elapsed Time: 00:00:20 Batch 52/60, Progress: |*.................................................| Elapsed Time: 00:00:20 Batch 52/60, Progress: |**................................................| Elapsed Time: 00:00:20 Batch 52/60, Progress: |**................................................| Elapsed Time: 00:00:20 Batch 52/60, Progress: |***...............................................| Elapsed Time: 00:00:20 Batch 52/60, Progress: |***...............................................| Elapsed Time: 00:00:20 Batch 52/60, Progress: |****..............................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |****..............................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*****.............................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*****.............................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |******............................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |******............................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*******...........................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*******...........................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |********..........................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |********..........................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*********.........................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*********.........................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**********........................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**********........................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***********.......................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***********.......................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |************......................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |************......................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*************.....................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*************.....................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**************....................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**************....................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***************...................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***************...................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |****************..................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |****************..................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*****************.................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*****************.................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |******************................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |******************................................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*******************...............................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*******************...............................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |********************..............................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |********************..............................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*********************.............................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*********************.............................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**********************............................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**********************............................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***********************...........................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***********************...........................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |************************..........................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |************************..........................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*************************.........................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*************************.........................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**************************........................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**************************........................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***************************.......................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***************************.......................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |****************************......................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |****************************......................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*****************************.....................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*****************************.....................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |******************************....................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |******************************....................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*******************************...................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*******************************...................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |********************************..................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |********************************..................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*********************************.................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*********************************.................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**********************************................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**********************************................| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***********************************...............| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***********************************...............| Elapsed Time: 00:00:21 Batch 52/60, Progress: |************************************..............| Elapsed Time: 00:00:21 Batch 52/60, Progress: |************************************..............| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*************************************.............| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*************************************.............| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**************************************............| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**************************************............| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***************************************...........| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***************************************...........| Elapsed Time: 00:00:21 Batch 52/60, Progress: |****************************************..........| Elapsed Time: 00:00:21 Batch 52/60, Progress: |****************************************..........| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*****************************************.........| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*****************************************.........| Elapsed Time: 00:00:21 Batch 52/60, Progress: |******************************************........| Elapsed Time: 00:00:21 Batch 52/60, Progress: |******************************************........| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*******************************************.......| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*******************************************.......| Elapsed Time: 00:00:21 Batch 52/60, Progress: |********************************************......| Elapsed Time: 00:00:21 Batch 52/60, Progress: |********************************************......| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*********************************************.....| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*********************************************.....| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**********************************************....| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**********************************************....| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***********************************************...| Elapsed Time: 00:00:21 Batch 52/60, Progress: |***********************************************...| Elapsed Time: 00:00:21 Batch 52/60, Progress: |************************************************..| Elapsed Time: 00:00:21 Batch 52/60, Progress: |************************************************..| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*************************************************.| Elapsed Time: 00:00:21 Batch 52/60, Progress: |*************************************************.| Elapsed Time: 00:00:21 Batch 52/60, Progress: |**************************************************| Elapsed Time: 00:00:21 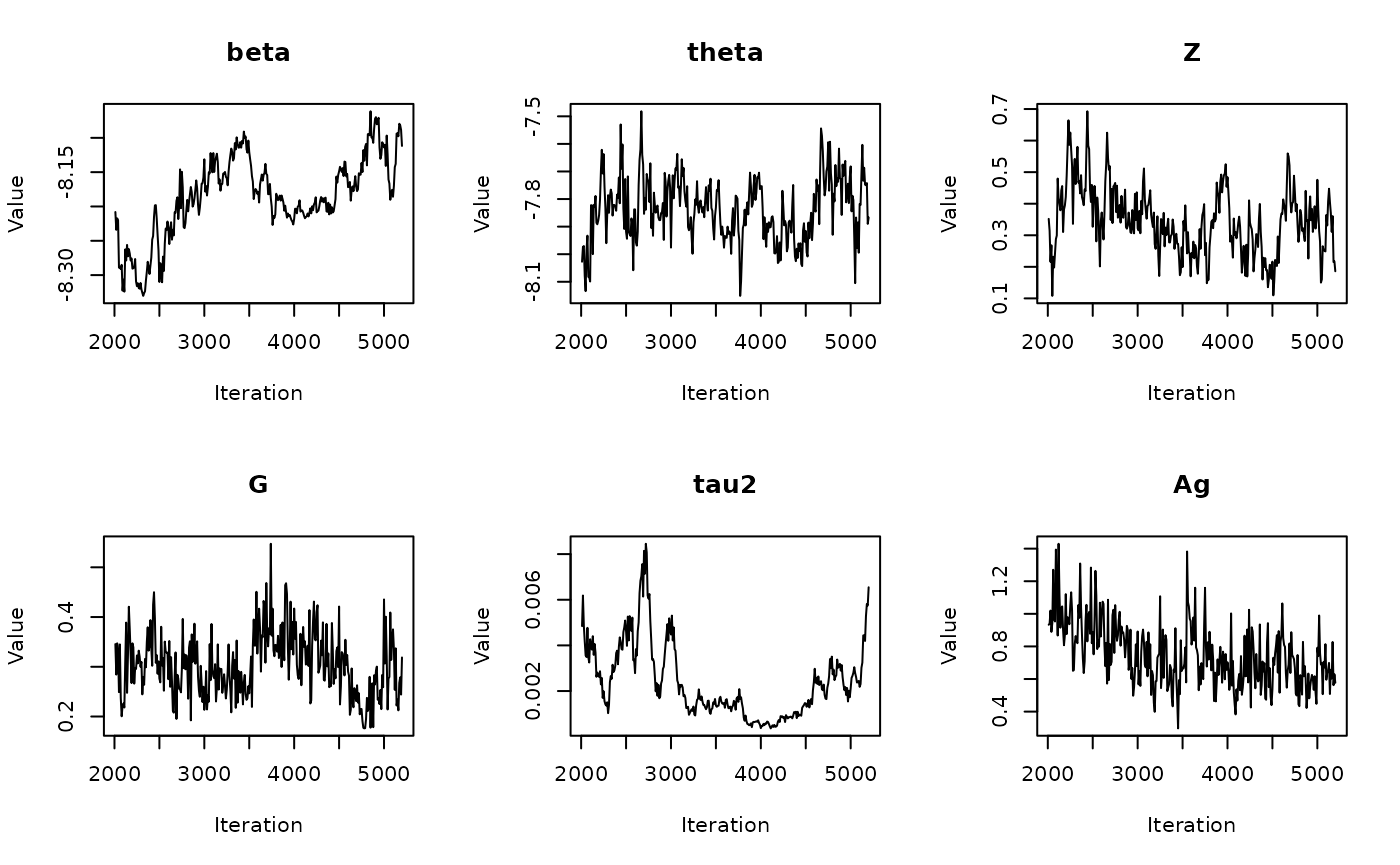
#> Batch 53/60, Progress: |..................................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |..................................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*.................................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*.................................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**................................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**................................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***...............................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***...............................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |****..............................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |****..............................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*****.............................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*****.............................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |******............................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |******............................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*******...........................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*******...........................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |********..........................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |********..........................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*********.........................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*********.........................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**********........................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**********........................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***********.......................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***********.......................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |************......................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |************......................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*************.....................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*************.....................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**************....................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**************....................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***************...................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***************...................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |****************..................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |****************..................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*****************.................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*****************.................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |******************................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |******************................................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*******************...............................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*******************...............................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |********************..............................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |********************..............................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*********************.............................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*********************.............................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**********************............................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**********************............................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***********************...........................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***********************...........................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |************************..........................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |************************..........................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*************************.........................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*************************.........................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**************************........................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**************************........................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***************************.......................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***************************.......................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |****************************......................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |****************************......................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*****************************.....................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*****************************.....................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |******************************....................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |******************************....................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*******************************...................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*******************************...................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |********************************..................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |********************************..................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*********************************.................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*********************************.................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**********************************................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**********************************................| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***********************************...............| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***********************************...............| Elapsed Time: 00:00:21 Batch 53/60, Progress: |************************************..............| Elapsed Time: 00:00:21 Batch 53/60, Progress: |************************************..............| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*************************************.............| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*************************************.............| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**************************************............| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**************************************............| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***************************************...........| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***************************************...........| Elapsed Time: 00:00:21 Batch 53/60, Progress: |****************************************..........| Elapsed Time: 00:00:21 Batch 53/60, Progress: |****************************************..........| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*****************************************.........| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*****************************************.........| Elapsed Time: 00:00:21 Batch 53/60, Progress: |******************************************........| Elapsed Time: 00:00:21 Batch 53/60, Progress: |******************************************........| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*******************************************.......| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*******************************************.......| Elapsed Time: 00:00:21 Batch 53/60, Progress: |********************************************......| Elapsed Time: 00:00:21 Batch 53/60, Progress: |********************************************......| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*********************************************.....| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*********************************************.....| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**********************************************....| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**********************************************....| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***********************************************...| Elapsed Time: 00:00:21 Batch 53/60, Progress: |***********************************************...| Elapsed Time: 00:00:21 Batch 53/60, Progress: |************************************************..| Elapsed Time: 00:00:21 Batch 53/60, Progress: |************************************************..| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*************************************************.| Elapsed Time: 00:00:21 Batch 53/60, Progress: |*************************************************.| Elapsed Time: 00:00:21 Batch 53/60, Progress: |**************************************************| Elapsed Time: 00:00:21 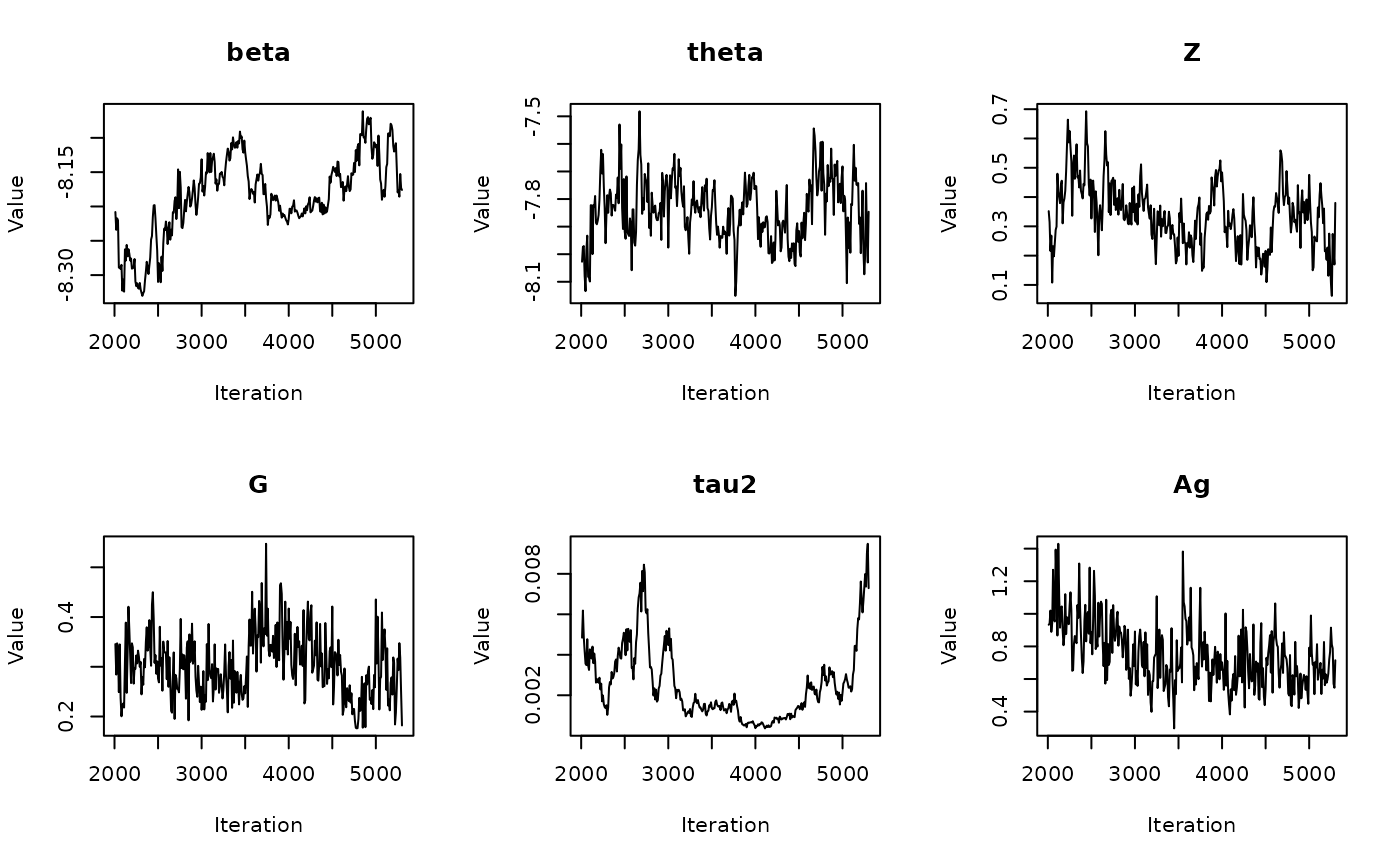
#> Batch 54/60, Progress: |..................................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |..................................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*.................................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*.................................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**................................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**................................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***...............................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***...............................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |****..............................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |****..............................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*****.............................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*****.............................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |******............................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |******............................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*******...........................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*******...........................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |********..........................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |********..........................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*********.........................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*********.........................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**********........................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**********........................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***********.......................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***********.......................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |************......................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |************......................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*************.....................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*************.....................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**************....................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**************....................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***************...................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***************...................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |****************..................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |****************..................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*****************.................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*****************.................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |******************................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |******************................................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*******************...............................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*******************...............................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |********************..............................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |********************..............................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*********************.............................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*********************.............................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**********************............................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**********************............................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***********************...........................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***********************...........................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |************************..........................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |************************..........................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*************************.........................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*************************.........................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**************************........................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |**************************........................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***************************.......................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |***************************.......................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |****************************......................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |****************************......................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*****************************.....................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*****************************.....................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |******************************....................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |******************************....................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*******************************...................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |*******************************...................| Elapsed Time: 00:00:21 Batch 54/60, Progress: |********************************..................| Elapsed Time: 00:00:22 Batch 54/60, Progress: |********************************..................| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*********************************.................| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*********************************.................| Elapsed Time: 00:00:22 Batch 54/60, Progress: |**********************************................| Elapsed Time: 00:00:22 Batch 54/60, Progress: |**********************************................| Elapsed Time: 00:00:22 Batch 54/60, Progress: |***********************************...............| Elapsed Time: 00:00:22 Batch 54/60, Progress: |***********************************...............| Elapsed Time: 00:00:22 Batch 54/60, Progress: |************************************..............| Elapsed Time: 00:00:22 Batch 54/60, Progress: |************************************..............| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*************************************.............| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*************************************.............| Elapsed Time: 00:00:22 Batch 54/60, Progress: |**************************************............| Elapsed Time: 00:00:22 Batch 54/60, Progress: |**************************************............| Elapsed Time: 00:00:22 Batch 54/60, Progress: |***************************************...........| Elapsed Time: 00:00:22 Batch 54/60, Progress: |***************************************...........| Elapsed Time: 00:00:22 Batch 54/60, Progress: |****************************************..........| Elapsed Time: 00:00:22 Batch 54/60, Progress: |****************************************..........| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*****************************************.........| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*****************************************.........| Elapsed Time: 00:00:22 Batch 54/60, Progress: |******************************************........| Elapsed Time: 00:00:22 Batch 54/60, Progress: |******************************************........| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*******************************************.......| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*******************************************.......| Elapsed Time: 00:00:22 Batch 54/60, Progress: |********************************************......| Elapsed Time: 00:00:22 Batch 54/60, Progress: |********************************************......| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*********************************************.....| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*********************************************.....| Elapsed Time: 00:00:22 Batch 54/60, Progress: |**********************************************....| Elapsed Time: 00:00:22 Batch 54/60, Progress: |**********************************************....| Elapsed Time: 00:00:22 Batch 54/60, Progress: |***********************************************...| Elapsed Time: 00:00:22 Batch 54/60, Progress: |***********************************************...| Elapsed Time: 00:00:22 Batch 54/60, Progress: |************************************************..| Elapsed Time: 00:00:22 Batch 54/60, Progress: |************************************************..| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*************************************************.| Elapsed Time: 00:00:22 Batch 54/60, Progress: |*************************************************.| Elapsed Time: 00:00:22 Batch 54/60, Progress: |**************************************************| Elapsed Time: 00:00:22 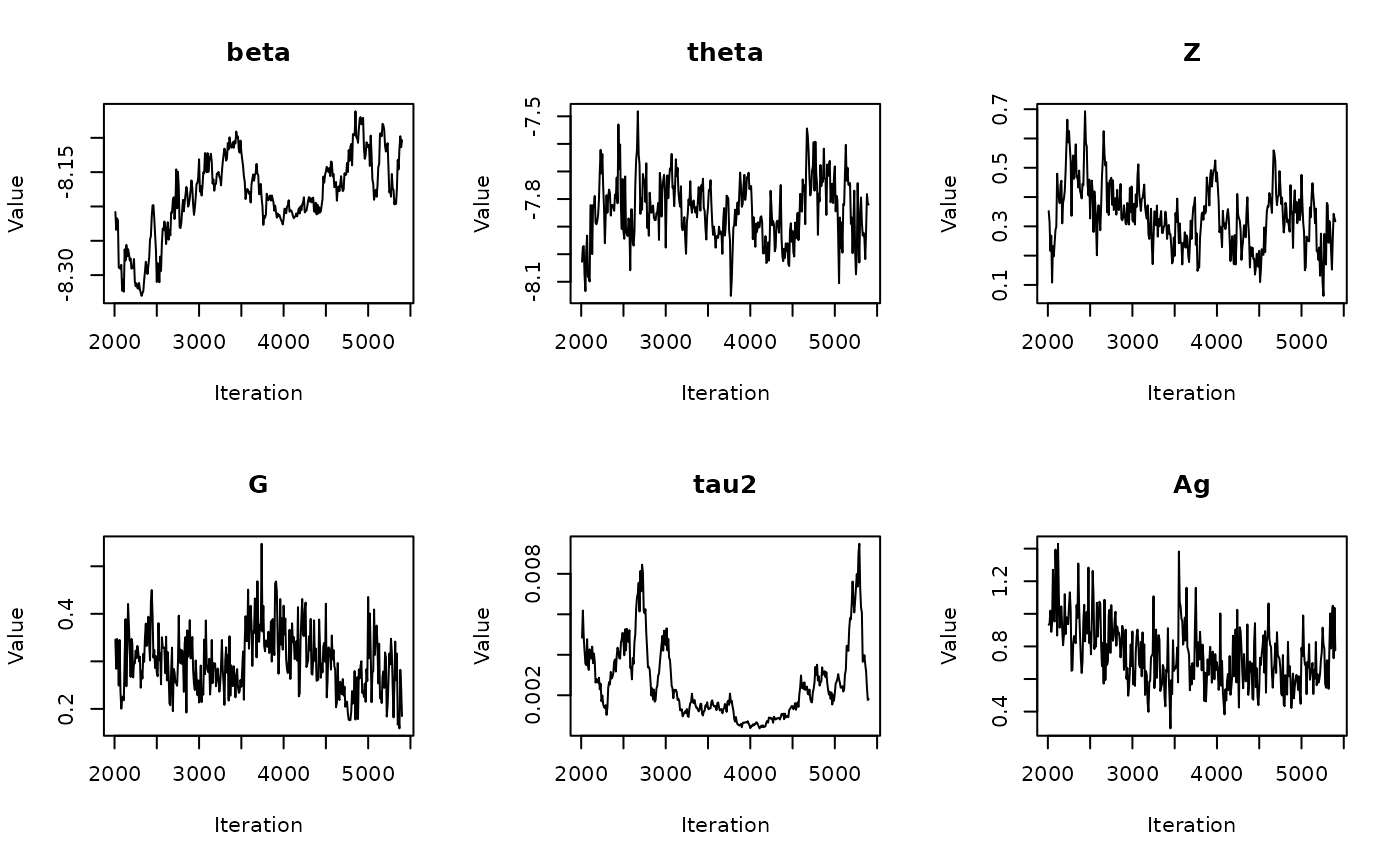
#> Batch 55/60, Progress: |..................................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |..................................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*.................................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*.................................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**................................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**................................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***...............................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***...............................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |****..............................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |****..............................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*****.............................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*****.............................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |******............................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |******............................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*******...........................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*******...........................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |********..........................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |********..........................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*********.........................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*********.........................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**********........................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**********........................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***********.......................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***********.......................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |************......................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |************......................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*************.....................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*************.....................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**************....................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**************....................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***************...................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***************...................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |****************..................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |****************..................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*****************.................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*****************.................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |******************................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |******************................................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*******************...............................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*******************...............................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |********************..............................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |********************..............................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*********************.............................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*********************.............................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**********************............................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**********************............................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***********************...........................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***********************...........................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |************************..........................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |************************..........................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*************************.........................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*************************.........................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**************************........................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**************************........................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***************************.......................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***************************.......................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |****************************......................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |****************************......................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*****************************.....................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*****************************.....................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |******************************....................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |******************************....................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*******************************...................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*******************************...................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |********************************..................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |********************************..................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*********************************.................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*********************************.................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**********************************................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**********************************................| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***********************************...............| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***********************************...............| Elapsed Time: 00:00:22 Batch 55/60, Progress: |************************************..............| Elapsed Time: 00:00:22 Batch 55/60, Progress: |************************************..............| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*************************************.............| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*************************************.............| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**************************************............| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**************************************............| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***************************************...........| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***************************************...........| Elapsed Time: 00:00:22 Batch 55/60, Progress: |****************************************..........| Elapsed Time: 00:00:22 Batch 55/60, Progress: |****************************************..........| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*****************************************.........| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*****************************************.........| Elapsed Time: 00:00:22 Batch 55/60, Progress: |******************************************........| Elapsed Time: 00:00:22 Batch 55/60, Progress: |******************************************........| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*******************************************.......| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*******************************************.......| Elapsed Time: 00:00:22 Batch 55/60, Progress: |********************************************......| Elapsed Time: 00:00:22 Batch 55/60, Progress: |********************************************......| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*********************************************.....| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*********************************************.....| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**********************************************....| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**********************************************....| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***********************************************...| Elapsed Time: 00:00:22 Batch 55/60, Progress: |***********************************************...| Elapsed Time: 00:00:22 Batch 55/60, Progress: |************************************************..| Elapsed Time: 00:00:22 Batch 55/60, Progress: |************************************************..| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*************************************************.| Elapsed Time: 00:00:22 Batch 55/60, Progress: |*************************************************.| Elapsed Time: 00:00:22 Batch 55/60, Progress: |**************************************************| Elapsed Time: 00:00:22 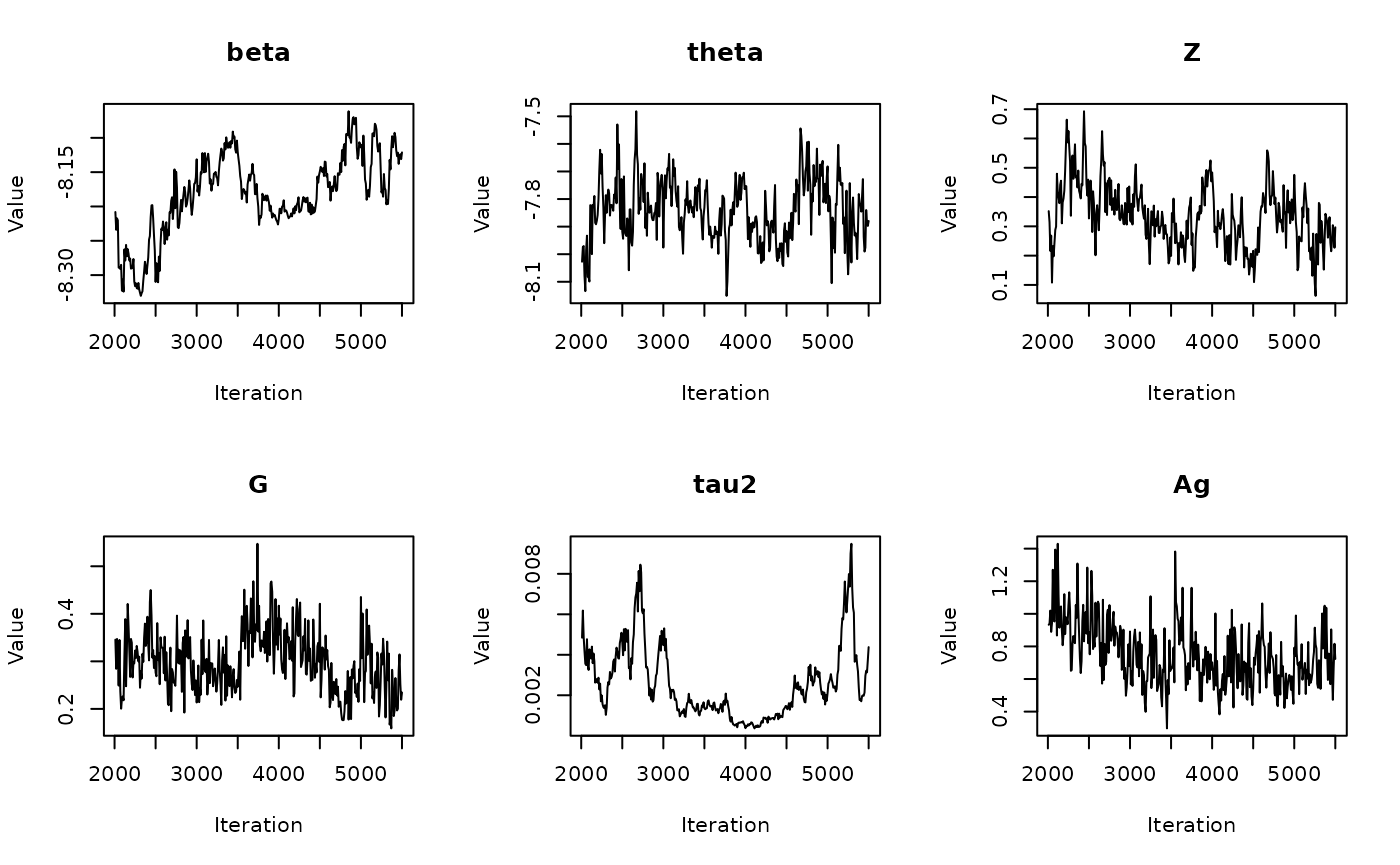
#> Batch 56/60, Progress: |..................................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |..................................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*.................................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*.................................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**................................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**................................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***...............................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***...............................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |****..............................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |****..............................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*****.............................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*****.............................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |******............................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |******............................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*******...........................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*******...........................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |********..........................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |********..........................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*********.........................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*********.........................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**********........................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**********........................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***********.......................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***********.......................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |************......................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |************......................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*************.....................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*************.....................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**************....................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**************....................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***************...................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***************...................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |****************..................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |****************..................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*****************.................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*****************.................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |******************................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |******************................................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*******************...............................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*******************...............................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |********************..............................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |********************..............................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*********************.............................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*********************.............................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**********************............................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**********************............................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***********************...........................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***********************...........................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |************************..........................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |************************..........................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*************************.........................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*************************.........................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**************************........................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**************************........................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***************************.......................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***************************.......................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |****************************......................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |****************************......................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*****************************.....................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*****************************.....................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |******************************....................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |******************************....................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*******************************...................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*******************************...................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |********************************..................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |********************************..................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*********************************.................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*********************************.................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**********************************................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**********************************................| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***********************************...............| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***********************************...............| Elapsed Time: 00:00:22 Batch 56/60, Progress: |************************************..............| Elapsed Time: 00:00:22 Batch 56/60, Progress: |************************************..............| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*************************************.............| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*************************************.............| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**************************************............| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**************************************............| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***************************************...........| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***************************************...........| Elapsed Time: 00:00:22 Batch 56/60, Progress: |****************************************..........| Elapsed Time: 00:00:22 Batch 56/60, Progress: |****************************************..........| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*****************************************.........| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*****************************************.........| Elapsed Time: 00:00:22 Batch 56/60, Progress: |******************************************........| Elapsed Time: 00:00:22 Batch 56/60, Progress: |******************************************........| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*******************************************.......| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*******************************************.......| Elapsed Time: 00:00:22 Batch 56/60, Progress: |********************************************......| Elapsed Time: 00:00:22 Batch 56/60, Progress: |********************************************......| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*********************************************.....| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*********************************************.....| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**********************************************....| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**********************************************....| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***********************************************...| Elapsed Time: 00:00:22 Batch 56/60, Progress: |***********************************************...| Elapsed Time: 00:00:22 Batch 56/60, Progress: |************************************************..| Elapsed Time: 00:00:22 Batch 56/60, Progress: |************************************************..| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*************************************************.| Elapsed Time: 00:00:22 Batch 56/60, Progress: |*************************************************.| Elapsed Time: 00:00:22 Batch 56/60, Progress: |**************************************************| Elapsed Time: 00:00:22 
#> Batch 57/60, Progress: |..................................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |..................................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*.................................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*.................................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**................................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**................................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***...............................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***...............................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |****..............................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |****..............................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*****.............................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*****.............................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |******............................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |******............................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*******...........................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*******...........................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |********..........................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |********..........................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*********.........................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*********.........................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**********........................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**********........................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***********.......................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***********.......................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |************......................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |************......................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*************.....................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*************.....................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**************....................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**************....................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***************...................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***************...................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |****************..................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |****************..................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*****************.................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*****************.................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |******************................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |******************................................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*******************...............................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*******************...............................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |********************..............................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |********************..............................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*********************.............................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*********************.............................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**********************............................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**********************............................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***********************...........................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***********************...........................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |************************..........................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |************************..........................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*************************.........................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*************************.........................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**************************........................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**************************........................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***************************.......................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***************************.......................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |****************************......................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |****************************......................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*****************************.....................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*****************************.....................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |******************************....................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |******************************....................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*******************************...................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*******************************...................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |********************************..................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |********************************..................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*********************************.................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*********************************.................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**********************************................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**********************************................| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***********************************...............| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***********************************...............| Elapsed Time: 00:00:23 Batch 57/60, Progress: |************************************..............| Elapsed Time: 00:00:23 Batch 57/60, Progress: |************************************..............| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*************************************.............| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*************************************.............| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**************************************............| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**************************************............| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***************************************...........| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***************************************...........| Elapsed Time: 00:00:23 Batch 57/60, Progress: |****************************************..........| Elapsed Time: 00:00:23 Batch 57/60, Progress: |****************************************..........| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*****************************************.........| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*****************************************.........| Elapsed Time: 00:00:23 Batch 57/60, Progress: |******************************************........| Elapsed Time: 00:00:23 Batch 57/60, Progress: |******************************************........| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*******************************************.......| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*******************************************.......| Elapsed Time: 00:00:23 Batch 57/60, Progress: |********************************************......| Elapsed Time: 00:00:23 Batch 57/60, Progress: |********************************************......| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*********************************************.....| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*********************************************.....| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**********************************************....| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**********************************************....| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***********************************************...| Elapsed Time: 00:00:23 Batch 57/60, Progress: |***********************************************...| Elapsed Time: 00:00:23 Batch 57/60, Progress: |************************************************..| Elapsed Time: 00:00:23 Batch 57/60, Progress: |************************************************..| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*************************************************.| Elapsed Time: 00:00:23 Batch 57/60, Progress: |*************************************************.| Elapsed Time: 00:00:23 Batch 57/60, Progress: |**************************************************| Elapsed Time: 00:00:23 
#> Batch 58/60, Progress: |..................................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |..................................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*.................................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*.................................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**................................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**................................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***...............................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***...............................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |****..............................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |****..............................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*****.............................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*****.............................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |******............................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |******............................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*******...........................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*******...........................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |********..........................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |********..........................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*********.........................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*********.........................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**********........................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**********........................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***********.......................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***********.......................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |************......................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |************......................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*************.....................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*************.....................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**************....................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**************....................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***************...................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***************...................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |****************..................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |****************..................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*****************.................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*****************.................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |******************................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |******************................................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*******************...............................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*******************...............................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |********************..............................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |********************..............................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*********************.............................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*********************.............................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**********************............................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**********************............................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***********************...........................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***********************...........................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |************************..........................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |************************..........................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*************************.........................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*************************.........................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**************************........................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**************************........................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***************************.......................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***************************.......................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |****************************......................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |****************************......................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*****************************.....................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*****************************.....................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |******************************....................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |******************************....................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*******************************...................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*******************************...................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |********************************..................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |********************************..................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*********************************.................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*********************************.................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**********************************................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**********************************................| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***********************************...............| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***********************************...............| Elapsed Time: 00:00:23 Batch 58/60, Progress: |************************************..............| Elapsed Time: 00:00:23 Batch 58/60, Progress: |************************************..............| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*************************************.............| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*************************************.............| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**************************************............| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**************************************............| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***************************************...........| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***************************************...........| Elapsed Time: 00:00:23 Batch 58/60, Progress: |****************************************..........| Elapsed Time: 00:00:23 Batch 58/60, Progress: |****************************************..........| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*****************************************.........| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*****************************************.........| Elapsed Time: 00:00:23 Batch 58/60, Progress: |******************************************........| Elapsed Time: 00:00:23 Batch 58/60, Progress: |******************************************........| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*******************************************.......| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*******************************************.......| Elapsed Time: 00:00:23 Batch 58/60, Progress: |********************************************......| Elapsed Time: 00:00:23 Batch 58/60, Progress: |********************************************......| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*********************************************.....| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*********************************************.....| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**********************************************....| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**********************************************....| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***********************************************...| Elapsed Time: 00:00:23 Batch 58/60, Progress: |***********************************************...| Elapsed Time: 00:00:23 Batch 58/60, Progress: |************************************************..| Elapsed Time: 00:00:23 Batch 58/60, Progress: |************************************************..| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*************************************************.| Elapsed Time: 00:00:23 Batch 58/60, Progress: |*************************************************.| Elapsed Time: 00:00:23 Batch 58/60, Progress: |**************************************************| Elapsed Time: 00:00:23 
#> Batch 59/60, Progress: |..................................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |..................................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*.................................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*.................................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |**................................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |**................................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |***...............................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |***...............................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |****..............................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |****..............................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*****.............................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*****.............................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |******............................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |******............................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*******...........................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*******...........................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |********..........................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |********..........................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*********.........................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*********.........................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |**********........................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |**********........................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |***********.......................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |***********.......................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |************......................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |************......................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*************.....................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*************.....................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |**************....................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |**************....................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |***************...................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |***************...................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |****************..................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |****************..................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*****************.................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*****************.................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |******************................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |******************................................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*******************...............................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |*******************...............................| Elapsed Time: 00:00:23 Batch 59/60, Progress: |********************..............................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |********************..............................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*********************.............................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*********************.............................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**********************............................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**********************............................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***********************...........................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***********************...........................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |************************..........................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |************************..........................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*************************.........................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*************************.........................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**************************........................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**************************........................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***************************.......................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***************************.......................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |****************************......................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |****************************......................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*****************************.....................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*****************************.....................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |******************************....................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |******************************....................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*******************************...................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*******************************...................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |********************************..................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |********************************..................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*********************************.................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*********************************.................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**********************************................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**********************************................| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***********************************...............| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***********************************...............| Elapsed Time: 00:00:24 Batch 59/60, Progress: |************************************..............| Elapsed Time: 00:00:24 Batch 59/60, Progress: |************************************..............| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*************************************.............| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*************************************.............| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**************************************............| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**************************************............| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***************************************...........| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***************************************...........| Elapsed Time: 00:00:24 Batch 59/60, Progress: |****************************************..........| Elapsed Time: 00:00:24 Batch 59/60, Progress: |****************************************..........| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*****************************************.........| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*****************************************.........| Elapsed Time: 00:00:24 Batch 59/60, Progress: |******************************************........| Elapsed Time: 00:00:24 Batch 59/60, Progress: |******************************************........| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*******************************************.......| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*******************************************.......| Elapsed Time: 00:00:24 Batch 59/60, Progress: |********************************************......| Elapsed Time: 00:00:24 Batch 59/60, Progress: |********************************************......| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*********************************************.....| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*********************************************.....| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**********************************************....| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**********************************************....| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***********************************************...| Elapsed Time: 00:00:24 Batch 59/60, Progress: |***********************************************...| Elapsed Time: 00:00:24 Batch 59/60, Progress: |************************************************..| Elapsed Time: 00:00:24 Batch 59/60, Progress: |************************************************..| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*************************************************.| Elapsed Time: 00:00:24 Batch 59/60, Progress: |*************************************************.| Elapsed Time: 00:00:24 Batch 59/60, Progress: |**************************************************| Elapsed Time: 00:00:24 
#> Batch 60/60, Progress: |..................................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |..................................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*.................................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*.................................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**................................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**................................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***...............................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***...............................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |****..............................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |****..............................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*****.............................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*****.............................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |******............................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |******............................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*******...........................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*******...........................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |********..........................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |********..........................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*********.........................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*********.........................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**********........................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**********........................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***********.......................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***********.......................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |************......................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |************......................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*************.....................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*************.....................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**************....................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**************....................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***************...................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***************...................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |****************..................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |****************..................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*****************.................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*****************.................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |******************................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |******************................................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*******************...............................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*******************...............................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |********************..............................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |********************..............................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*********************.............................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*********************.............................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**********************............................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**********************............................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***********************...........................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***********************...........................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |************************..........................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |************************..........................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*************************.........................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*************************.........................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**************************........................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**************************........................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***************************.......................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***************************.......................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |****************************......................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |****************************......................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*****************************.....................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*****************************.....................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |******************************....................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |******************************....................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*******************************...................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*******************************...................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |********************************..................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |********************************..................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*********************************.................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*********************************.................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**********************************................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**********************************................| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***********************************...............| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***********************************...............| Elapsed Time: 00:00:24 Batch 60/60, Progress: |************************************..............| Elapsed Time: 00:00:24 Batch 60/60, Progress: |************************************..............| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*************************************.............| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*************************************.............| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**************************************............| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**************************************............| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***************************************...........| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***************************************...........| Elapsed Time: 00:00:24 Batch 60/60, Progress: |****************************************..........| Elapsed Time: 00:00:24 Batch 60/60, Progress: |****************************************..........| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*****************************************.........| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*****************************************.........| Elapsed Time: 00:00:24 Batch 60/60, Progress: |******************************************........| Elapsed Time: 00:00:24 Batch 60/60, Progress: |******************************************........| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*******************************************.......| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*******************************************.......| Elapsed Time: 00:00:24 Batch 60/60, Progress: |********************************************......| Elapsed Time: 00:00:24 Batch 60/60, Progress: |********************************************......| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*********************************************.....| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*********************************************.....| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**********************************************....| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**********************************************....| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***********************************************...| Elapsed Time: 00:00:24 Batch 60/60, Progress: |***********************************************...| Elapsed Time: 00:00:24 Batch 60/60, Progress: |************************************************..| Elapsed Time: 00:00:24 Batch 60/60, Progress: |************************************************..| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*************************************************.| Elapsed Time: 00:00:24 Batch 60/60, Progress: |*************************************************.| Elapsed Time: 00:00:24 Batch 60/60, Progress: |**************************************************| Elapsed Time: 00:00:24 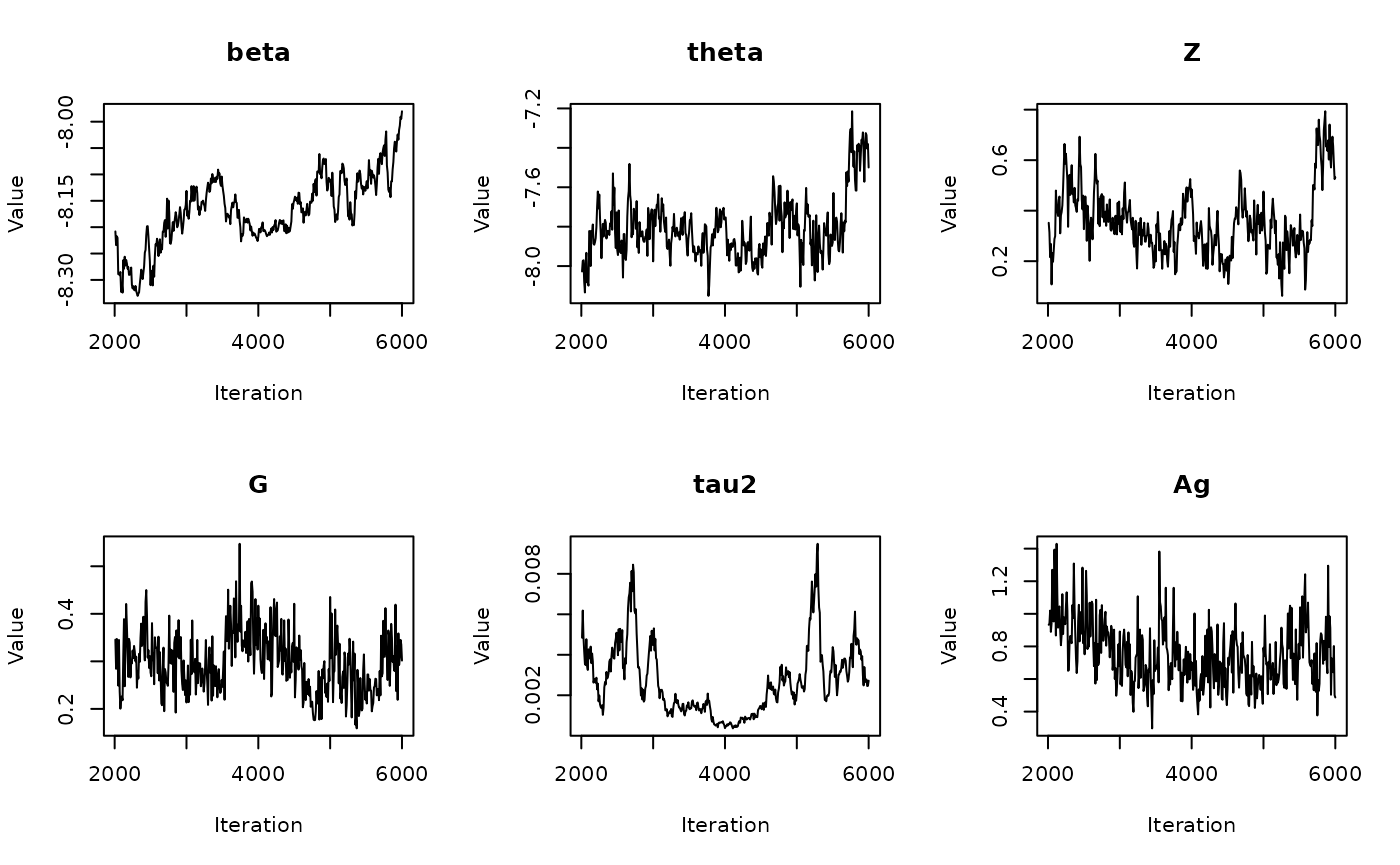
#>
#> Model finished at Tue Sep 16 20:25:05To get the medians, let’s reload our age-standardized data and
population array, then load our samples into
get_medians():
From here, we can map our estimates:
library(ggplot2)
est_35_64 <- medians[, "35-64", "1979"]
ggplot(mishp) +
geom_sf(aes(fill = est_35_64)) +
labs(
title = "Smoothed Myocardial Infarction Death Rates in MI, Ages 35-64, 1979",
fill = "Deaths per 100,000"
) +
scale_fill_viridis_c() +
theme_void()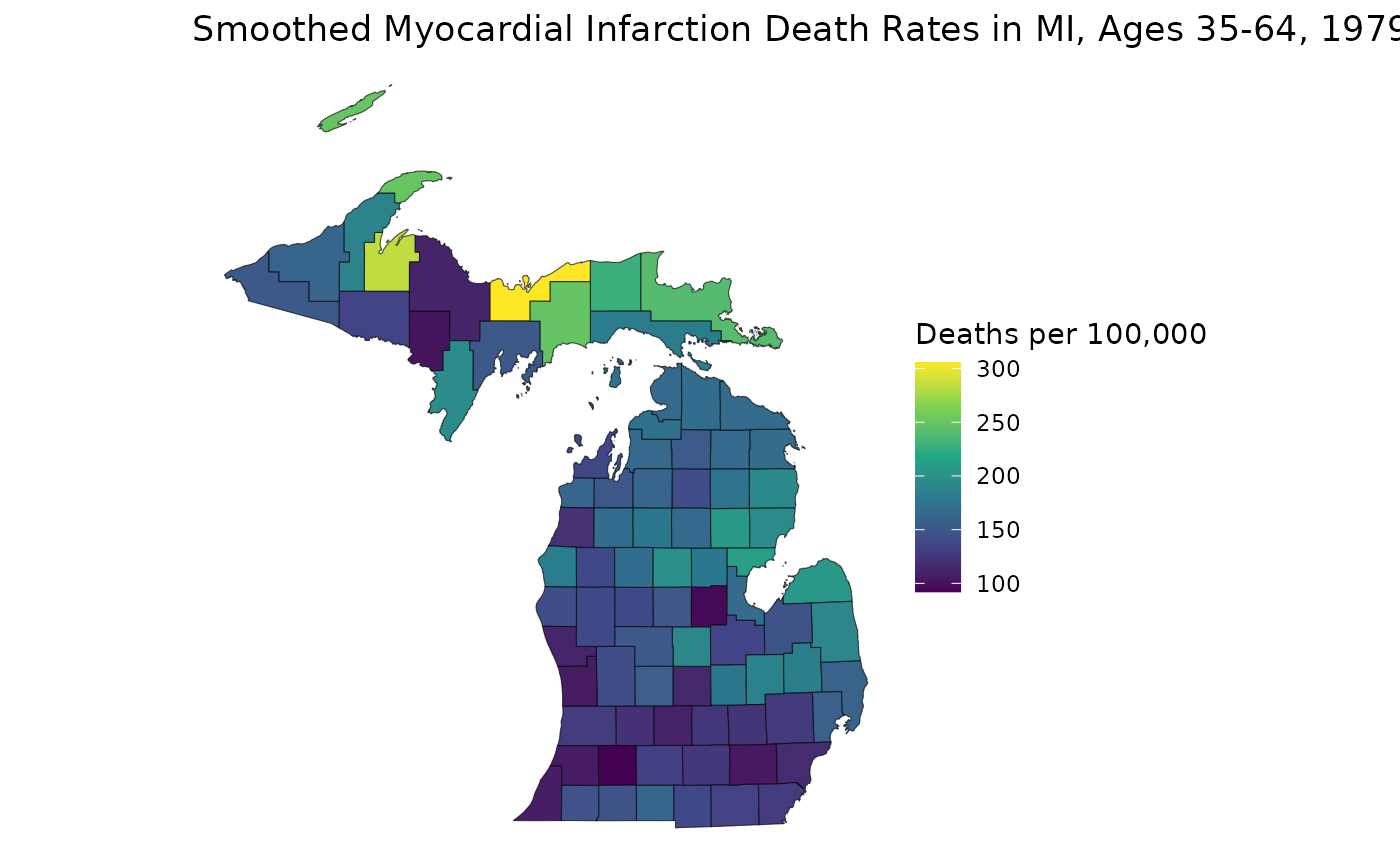
Recall, though, in the previous vignette, we discovered that some traceplots were not as stable (i.e., reliable) as others. How can we test for reliability in our estimates?
Estimate reliability
Reliability can be easily tested in CAR models using two criteria:
- Relative precision: In Quick, et al 2024, relative precision is measured as a ratio of the posterior median to its credible interval. If an estimate’s ratio is less than 1, then that estimate is considered unreliable at that level of credibility. Effectively, this means that unreliable estimates have a spread of samples larger than the value of the estimate itself; and
- Population counts: Though
RSTris designed to stabilize low-population regions, there is a limit to the amount of information the model can gather, and estimates from exceedingly low-population regions may be over-smoothed. Therefore, estimates from any region that fall below a specified threshold will be considered unreliable, regardless of relative precision. Use your judgment when setting this threshold depending on what kind of data you are working with: for example, 1,000 population is generally a good rule of thumb for mortality data, whereas an appropriate cutoff for birth data is closer to 100.
Let’s get some reliability metrics for our dataset. First, let’s
generate our relative precisions at 95% credibility using the
get_relative_precision() function and then create a
logical array that tells us which estimates
are unreliable:
rel_prec <- get_relative_precision(
output = theta,
medians = medians,
perc_ci = 0.95
)
low_rel_prec <- rel_prec < 1Now, let’s generate a similar logical array
for populations less than 1000 and use both of these criteria to create
a set of suppressed medians. A median will be suppressed if it meets
either of the two criteria:
low_population <- pop < 1000
medians_supp <- medians
medians_supp[low_rel_prec | low_population] <- NALooking at our dataset, we can see that most of our estimates meet both criteria! Certain counties, unfortunately, are too small to get reliable estimates for, but fortunately our estimates generally had high relative precision. Let’s now map our suppressed estimates again and see what changed:
est_35_64 <- medians_supp[, "35-64", "1979"]
ggplot(mishp) +
geom_sf(aes(fill = est_35_64)) +
labs(
title = "Smoothed Myocardial Infarction Death Rates in MI, Ages 35-64, 1979",
fill = "Deaths per 100,000"
) +
scale_fill_viridis_c() +
theme_void()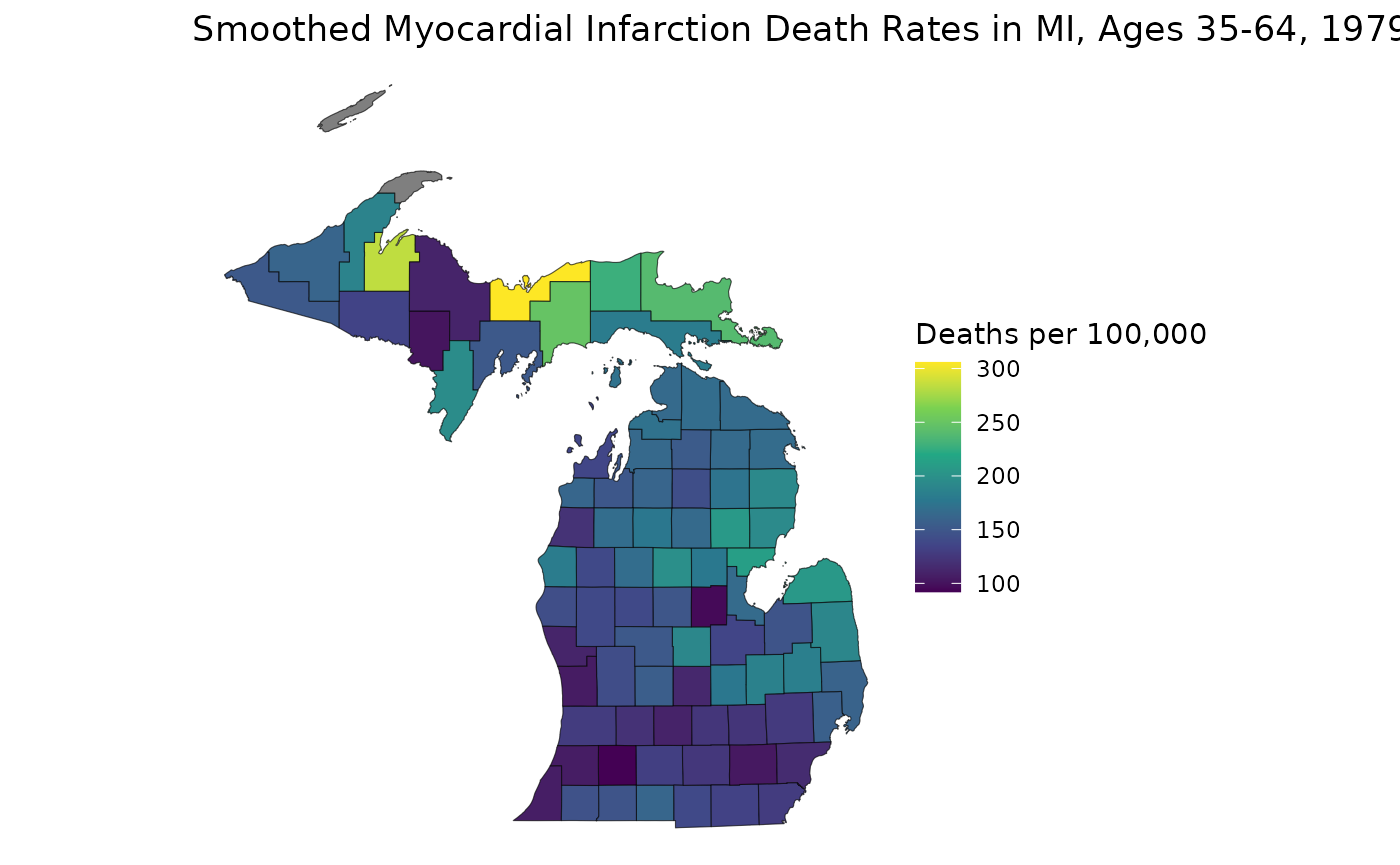
In this group in 1979, it seems only one region has been suppressed
(i.e., grayed out). This is because age-standardizing the samples after
running the model both helps to bolster our relative precisions and to
increase the total population in our groups, increasing values for both
suppression criteria. If we suppress our estimates in our more granular,
non-age-standardized theta samples, we will see that, even
with a small credible interval, many more counties are suppressed:
rel_prec <- get_relative_precision(
output = theta,
medians = medians,
perc_ci = 0.5
)
low_rel_prec <- rel_prec < 1
medians_supp <- medians
medians_supp[low_rel_prec | low_population] <- NA
est_35_44 <- medians_supp[, "35-44", "1979"]
ggplot(mishp) +
geom_sf(aes(fill = est_35_44)) +
labs(
title = "Smoothed Myocardial Infarction Death Rates in MI, Ages 35-44, 1979",
subtitle = "Relative Precision based on 50% Credible Interval",
fill = "Deaths per 100,000"
) +
scale_fill_viridis_c() +
theme_void()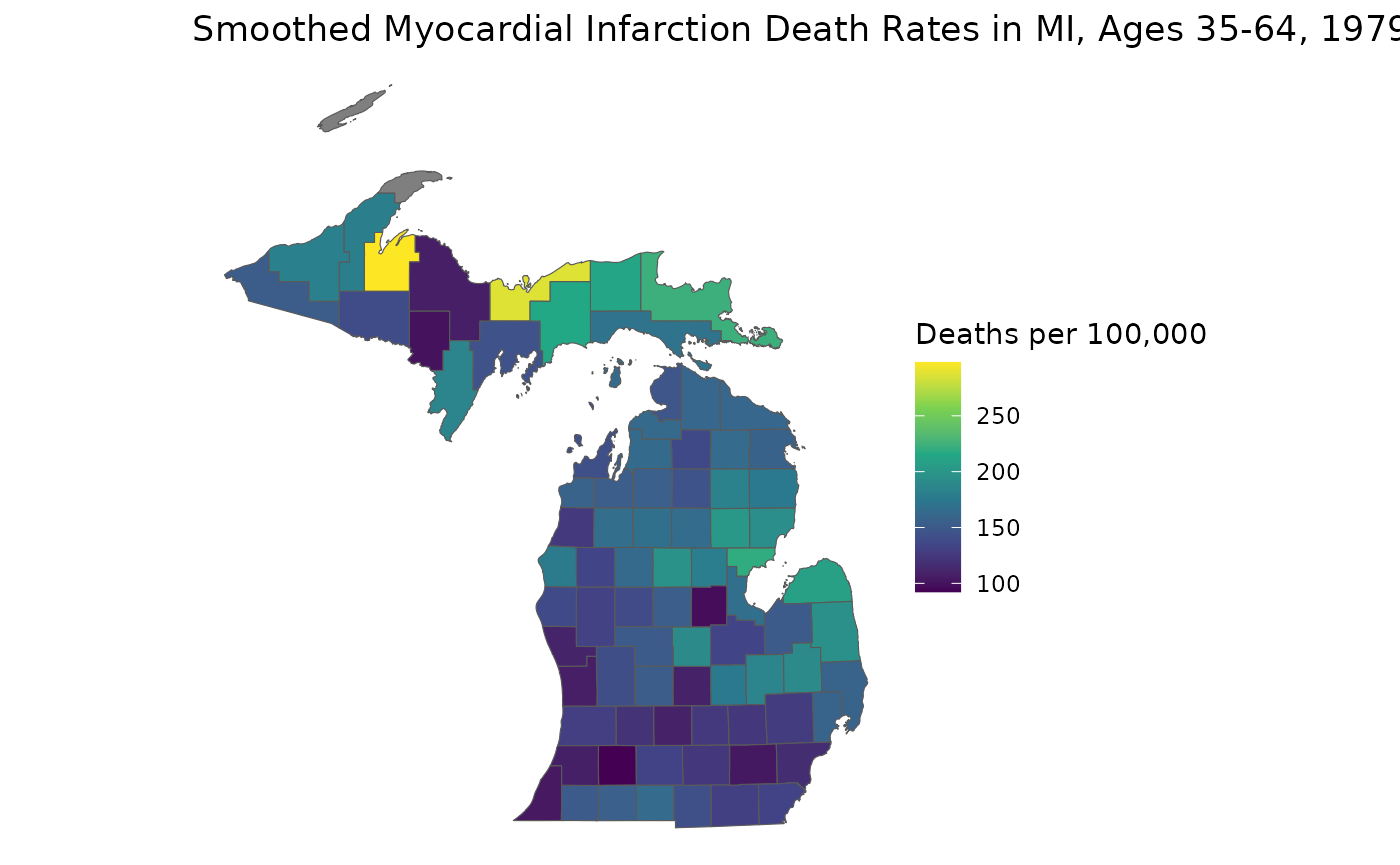
As we widen our credible interval, the reliability criteria will become more conservative and suppress more counties:
rel_prec <- get_relative_precision(
output = theta,
medians = medians,
perc_ci = 0.995
)
low_rel_prec <- rel_prec < 1
medians_supp <- medians
medians_supp[low_rel_prec | low_population] <- NA
est_35_44 <- medians_supp[, "35-44", "1979"]
ggplot(mishp) +
geom_sf(aes(fill = est_35_44)) +
labs(
title = "Smoothed Myocardial Infarction Death Rates in MI, Ages 35-44, 1979",
subtitle = "Relative Precision based on 99.5% Credible Interval",
fill = "Deaths per 100,000"
) +
scale_fill_viridis_c() +
theme_void()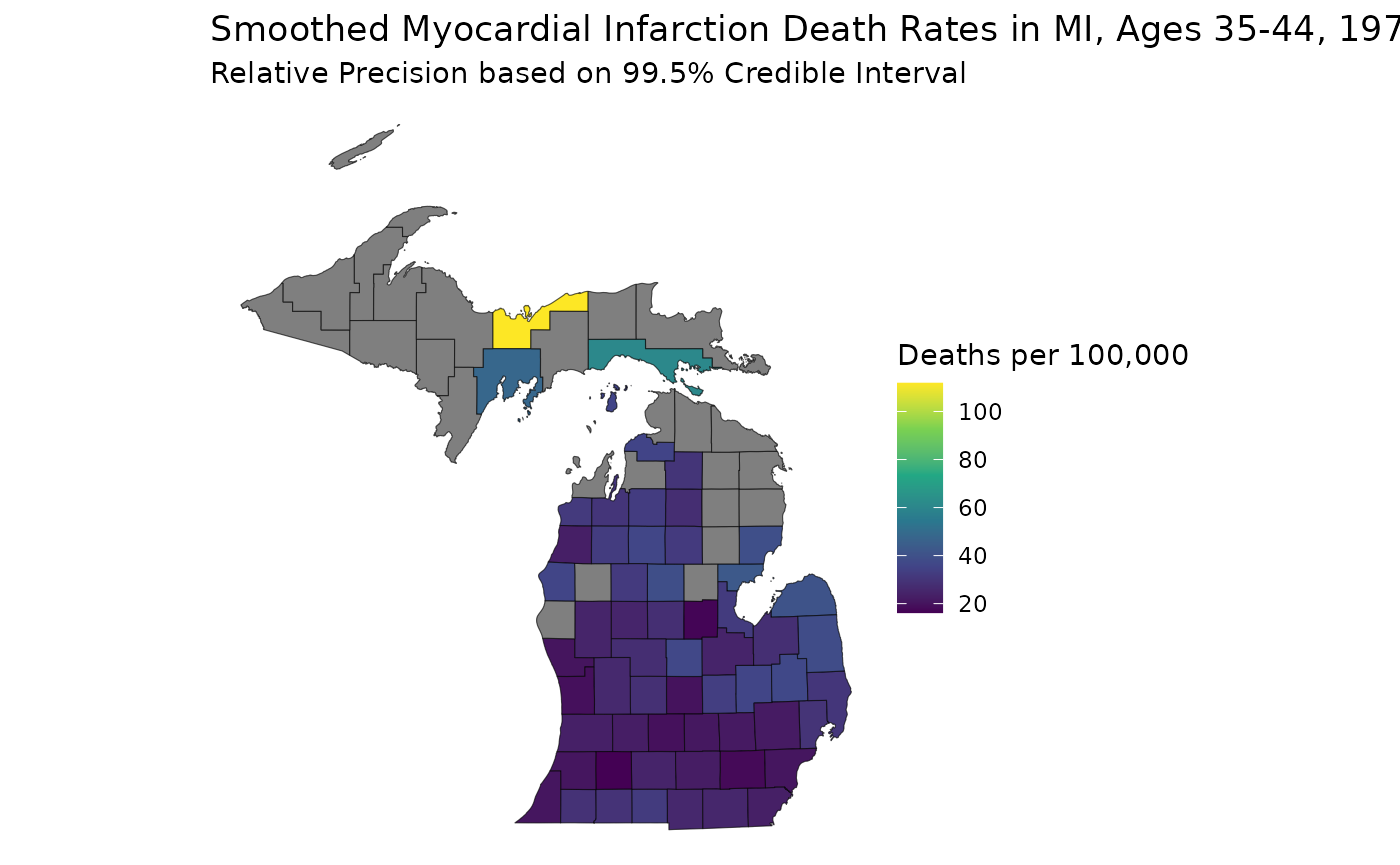
If we continue increasing our CI width from 0.50 to 0.95 to 0.99 and 0.995, our estimates must be more precise and more counties become grayed out. It is important to find a good balance between credible interval choice and displaying of estimates. Usually, a 95% credible interval provides a happy medium and is the value that is traditionally used.
Final thoughts
In this vignette, we explored the get_medians()
function, investigated measures of reliability, and observed how
reliability measures changed which data are suppressed. This vignette
concludes the main sections on using the functions in the
RSTr package. After reading these, you should be able to
prepare your event and adjacency data, configure your model as
necessary, and determine which estimates are reliable. If you are
interested in learning more about how the MSTCAR model itself works,
read vignette("RSTr-models").